Матричная запись системы линейных уравнений и решение системы в матричной форме.

Матричная запись системы линейных уравнений , где — основная матрица системы, и — столбцы свободных членов и решений системы соответственно:

Решение системы в матричной форме. Первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A^-1, получим A^-1AX= A^-1B, откуда EX=X=A^-1B. Следовательно, матрица-решение X легко находится как произведение A^-1 и B.

7. Система трёх линейных уравнений с тремя неизвестными. Правило Крамера.

Система трех линейных уравнений с тремя неизвестными имеет вид

Правило Крамера.

Дана система линейных уравнений:

Определители:

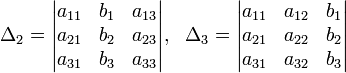
Решение:

Решение систем линейных алгебраических уравнений методом Гаусса.

Метод Гаусса состоит в последовательном исключении неизвестных (то есть приведение матрицы к треугольному или трапециевидному виду).

Ранг матрицы, его вычисление. Теорема Кронекера-Капелли.

Ранг матрицы, его вычисление. Одним из способов вычисления ранга матрицы является метод окаймления миноров.

Другой способ вычисления ранга матрицы основан на применении элементарных преобразований матрицы и использовании следующих утверждений.

1) Ранг ступенчатой матрицы равен количеству её ненулевых строк.

2) Элементарные преобразования матрицы не изменяют её ранг.

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Дата добавления: 2015-10-24