Определители второго и третьего порядков, их свойства.

Экзамен по математике. I семестр.

Тема 1. Матрицы и определители. Решение и исследование систем линейных алгебраических уравнений

Матрица. Различные виды матриц.

Матрицей размера или порядка m n называется прямоугольная таблица чисел, имеющая m строк и n столбцов.

Виды:

Матрица называется квадратной, если m=n.

Квадратная матрица, у которой все элементы, стоящие вне главной диагонали, равны нулю, называется диагональной.

Квадратная матрица, у которой все элементы выше или ниже главной диагонали равны 0, называется треугольной.

Если в прямоугольной матрице элементы, стоящие ниже главной диагонали, равны 0, то матрица называется трапециевидной.

Матрица называется транспортированной, если строки поменять на соответствующие столбцы.

Если в диагональной матрице все элементы, стоящие на главной диагонали равны 1, то матрица называется единичной.

Матрица, состоящая из 0, называется нулевой матрицей.

Квадратная матрица называется вырожденной, если определитель этой матрицы равен 0.

Квадратная матрица называется невырожденной, если определитель этой матрицы не равен 0.

Сумма, разность и умножение матриц. Свойства сложения и умножения матриц.

Суммой матриц и одинаковых размеров называется матрица 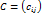тех же размеров, у которой Обозначение: C = А + В.

Свойства сложения матриц: А + В = В + А, (А + В) + С = A + (B + C), А + 0 = A, А + (-A) = 0, A, B, C.
Вычитание матриц: А - В = А + (-В).
Произведением матрицы размером на матрицу размером называется матрица размером у которой Обозначение: C = AB.

Свойства AE = EA = A, AO = OA = O, (AB)D = A(BD), (AB) = ( A)B = A( B), (A + B)D=AD + BD, D(A + B) = DA + DB (при условии, что указанные операции имеют смысл).

Для квадратных матриц А и B, вообще говоря,

Определители второго и третьего порядков, их свойства.

Определителем второго порядка называется число равное произведению элементов стоящих на главной диагонали минус произведение элементов стоящих на побочной диагонали.

Определителем третьего порядка называется число равное

и обозначаемое символом

Итак, по определению

Свойства.

1) Транспонированный определитель равен данному.

2) Определитель, имеющий две одинаковые строки (столбца) равен нулю.

3) Постоянный множитель строки или столбца можно выносить за знак определителя.

4) Определитель, имеющий 2 пропорциональные строки или столбца равен 0.

5) Определитель, имеющий строку (столбец) состоящей из нулей равен 0.

6) Если в определителе поменять местами 2 соседние строки (столбца), то это равносильно умножению определителя на -1.

7) Величина определителя не изменится, если к элементам какой либо строки (столбца) прибавить элементы другой строки (столбца), умноженное на некоторое число.

8) Сумма произведений элементов какой либо строки или столбца на алгебраические дополнения другой строки или столбца равно 0.

Дата добавления: 2015-10-24