Исследование решений систем линейных алгебраических уравнений.

1) Δ ≠0 система имеет единственное решение

2) Δ=0, а хотя бы один из вспомогательных ≠0, то решений нет

3) Δ= Δ1= Δ2= Δ3=0 бесчисленное множество решений

Тема 2. Векторная алгебра

Основные понятия векторной алгебры. Линейные операции над векторами. Угол между векторами.

Вектор - это направленный отрезок, который имеет начало и конец.

Длиной ненулевого вектора называется длина отрезка AB.

Нулевой вектор — вектор, начало которого совпадает с его концом.

Орты – единичный вектор.

Чтобы сложить два вектора, нужно от конца одного из них отложить второй вектор; тогда сумма – это вектор с началом в начале первого вектора и концом в конце второго вектора: .

Разностью двух векторов и называется такой третий вектор , который равен сумме векторов и .

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

Прямоугольная система координат. Координаты векторов. Разложение вектора по базису.

Прямоугольная система координат – система плоских координат образованная двумя взаимноперпендикулярными прямыми линиями, называемыми осями координат x и y. Точка их пересечения называется началом или нулем системы координат. Ось абсцисс – OX, ось ординат – OY.

Координаты вектора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

Разложение вектора по базису имеет вид:

Направляющие косинусы векторов.

Направляющие косинусы вектора – это косинусы углов, которые вектор образует с положительными полуосями координат.

Чтобы найти направляющие косинусы вектора необходимо соответствующие координаты вектора поделить на модуль вектора.

Линейные операции над векторами в координатах. Условие коллинеарности векторов.

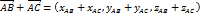
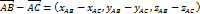
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

a={a_x; a_y; a_z} и b={b_x; b_y; b_z} коллинеарны если

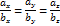
Дата добавления: 2015-10-24