
Читайте также:
|
1. Явное задание кривой. В этом случае кривая задается в виде  ,
,  , и длина ее дуги равна L=
, и длина ее дуги равна L=  .
.
2. Кривая в полярных координатах. Уравнение кривой имеет в этом случае вид  и длина ее дуги равна L=
и длина ее дуги равна L=  .
.
3. Параметрическое задании кривой. Пусть функции x (t) и y (t) имеют на отрезке  непрерывныепроизводные
непрерывныепроизводные  и
и  . Тогда длина дуги кривой
. Тогда длина дуги кривой
L=  .
.
Пример. Найдём длину дуги кривой (циклоиды), заданной на плоскости  параметрическими уравнениями
параметрическими уравнениями

 |
 ) и A(2
) и A(2  a;0) (соответствует
a;0) (соответствует 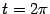 ).
).
Для функций f1(t)=a(t-sint) и f2(t)=a(1-cost) вычислим производные: 
Тогда искомая длина дуги равна

 |
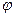 ) задана уравнением r=a
) задана уравнением r=a  (a>0). Поскольку функция f(
(a>0). Поскольку функция f(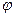 )=a
)=a  периодична с периодом
периодична с периодом  , достаточно рассматривать только значения аргумента
, достаточно рассматривать только значения аргумента 
 , при которых выражение
, при которых выражение  неотрицательно. Кривая имеет вид, изображённый на следующем рисунке.
неотрицательно. Кривая имеет вид, изображённый на следующем рисунке.
Найдём длину этой линии.
Имеем 
Поэтому искомая длина  равна
равна
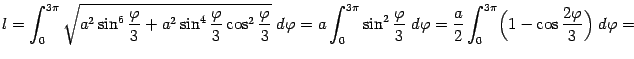

Нахождение объёма тела по площадям поперечных сечений
 Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными оси
Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными оси 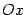 и проходящими через точки x
и проходящими через точки x  на ней. Площадь фигуры, образующейся в сечении, зависит от точки х, определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на
на ней. Площадь фигуры, образующейся в сечении, зависит от точки х, определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на 
 функцией
функцией  . Тогда объем части тела, находящейся между плоскостями х=а и х=в вычисляется по формуле
. Тогда объем части тела, находящейся между плоскостями х=а и х=в вычисляется по формуле 
Пример. Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса  :
: 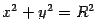 , горизонтальной плоскостью
, горизонтальной плоскостью  и наклонной плоскостью z=2y и лежащего выше горизонтальной плоскости
и наклонной плоскостью z=2y и лежащего выше горизонтальной плоскости  .
.
Очевидно, что рассматриваемое тело  проектируется на ось
проектируется на ось 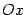 в отрезок
в отрезок  , а при x
, а при x 
 поперечное сечение тела представляет собою прямоугольный треугольник с катетами y и z=2y, где y можно выразить через x из уравнения цилиндра:
поперечное сечение тела представляет собою прямоугольный треугольник с катетами y и z=2y, где y можно выразить через x из уравнения цилиндра:
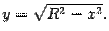
Поэтому площадь S(x) поперечного сечения такова:

Применяя формулу, находим объём тела  :
:

Дата добавления: 2015-10-30; просмотров: 186 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление площадей плоских фигур | | | Вычисление объемов тел вращения |