Квадратурная формула трапеций

Пусть снова взято разбиение отрезка . на части , где i=1,2…n. Приближённо заменим площадь под графиком y=f(x), лежащую над промежутком разбиения , на площадь трапеции, параллельными основаниями которой служат отрезки, задающие значения функции в концах промежутка, то есть f(xi-1)и f(xi) (см. рис.5).

Рис.5.

Тогда площадь такой трапеции равна, очевидно,

Суммируя все площади S_i, получаем квадратурную формулу трапеций:

Это та же формула, что была получена при комбинировании формул левых и правых прямоугольников, в которой мы обозначали правую часть через I_rl.

Заметим, что при подсчёте площади каждой очередной трапеции S_i достаточно вычислить значение функции f лишь в одной новой точке — в правом конце x_i очередного промежутка , поскольку точка x_i-1 была правым концом предыдущего отрезка и значение в этой точке уже было вычислено при нахождении площади предыдущей трапеции.

Если все отрезки разбиения выбираются одинаковой длины , то формула трапеций приобретает вид

Все значения функции f(x_i), кроме f(x₀)=f(a) и f(x_n)=f(b), встречаются в этой формуле по два раза. Поэтому, объединяя равные слагаемые, мы можем записать формулу трапеций в виде

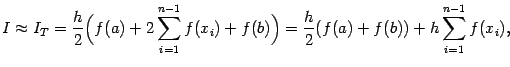
где x_i=a+ih, i=1,…,n-1.

Пусть функция f(x) имеет вторую производную f^//(x), сохраняющую знак на интервале (a;b). Как легко видно из предыдущего рисунка, характер ошибки этой квадратурной формулы таков: если f^//(x)<0, то есть если график y=f(x) является выпуклым кверху, то I>I_T, значит, ; если же f^//(x)>0 и график имеет выпуклость книзу, то I<I_T и .

Если сравнить это с изученными выше значениями ошибки формулы центральных прямоугольников, то мы видим, что для функций, вторая производная которых сохраняет знак на отрезке интегрирования, знаки ошибок и противоположны. Возникает желание соединить формулу трапеций и формулу центральных прямоугольников так, чтобы эти ошибки по возможности скомпенсировались. Для того, чтобы понять, какую комбинацию формул следует брать, нам нужно выяснить, какую величину имеют эти ошибки и в зависимости от выбора шага . Эти оценки ошибок имеют и самостоятельное значение, поскольку позволяют узнать точность полученного при применении соответствующей квадратурной формулы приближённого значения интеграла.

Дата добавления: 2015-10-30