Приложения определенного интеграла к решению некоторых задач механики и физики

Работа переменной силы. Рассмотрим движение материальной точки вдоль оси OX под действием переменной силы f, зависящей от положения точки x на оси, т.e. силы, являющейся функцией x. Тогда работа A, необходимая для перемещения материальной точки из позиции x = a в позицию x = b вычисляется по формуле:

Для вычисления силы давления жидкости используют закон Паскаля, согласно которому давление жидкости на площадку равно ее площади S, умноженной на глубину погружения h, на плотность ρ и ускорение силы тяжести g, т.е.

.

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность , то статические моменты этой дуги M_x и M_y относительно координатных осей Ox и Oy равны

;

моменты инерции I_Х и I_у относительно тех же осей Ох и Оу вычисляются по формулам

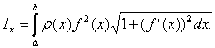
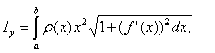
а координаты центра масс и — по формулам

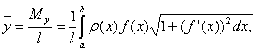
где l— масса дуги, т. е.

Пример 1. Найти статические моменты и моменты инерции относительно осей Ох и Оу дуги цепной линии y=chx при 0≤x≤1.

Если плотность не указана, предполагается, что кривая однородна и . Имеем: Следовательно,

Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти. Имеем:

Отсюда получаем:

В приложениях часто оказывается полезной следующая ТеоремаГульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

Пример 3. Найти координаты центра масс полуокружности

Вследствие симметрии 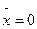. При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна 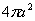, а длина полуокружности равна па. По теореме Гульдена имеем 4

Отсюда 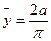, т.е. центр масс C имеет координаты C .

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах.

Пример 4. Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Так как путь, пройденный телом со скоростью v(t) за отрезок времени [t₁,t₂], выражается интегралом

то имеем:

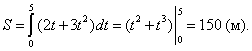
Пример. Найдём площадь 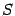ограниченной области, лежащей между осью 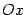и линией y=x³-x. Поскольку

линия пересекает ось 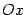в трёх точка: x₁=-1, x₂=0, x₃=1.

Ограниченная область между линией и осью 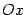проектируется на отрезок , причём на отрезке , линия y=x³-x идёт выше оси 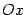(то есть линии y=0, а на - ниже. Поэтому площадь области можно подсчитать так:

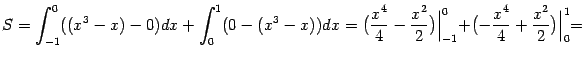
Пример. Найдём площадь 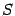области, заключённой между первым и вторым витком спирали Архимеда r=a 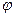(a>0) и отрезком горизонтальной оси .

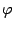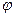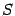Первый виток спирали соответствует изменению угла в пределах от 0 до , а второй — от до . Чтобы привести изменение аргумента к одному промежутку, запишем уравнение второго витка спирали в виде , . Тогда площадь можно будет найти по формуле, положив и :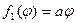

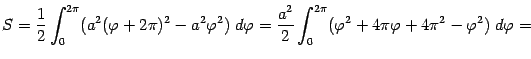
Пример. Найдём объём тела, ограниченного поверхностью вращения линии y=4x-x² вокруг ос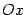и (при ).

Для вычисления объёма тела вращения применим формулу

Имеем:

Пример. Вычислим длину дуги линии y=lncosx, расположенной между прямыми и .

Так как

и

(мы взяли в качестве значения корня 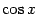, а не -cosx, поскольку cosx >0 при , длина дуги равна

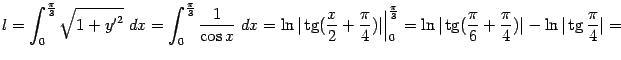
Ответ: .

Пример. Вычислим площадь Q поверхности вращения, полученной при вращении дуги циклоиды x=t-sint; y=1-cost, при 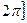, вокруг оси .

Для вычисления применим формулу:

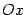Имеем: 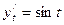, так что

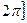Для перехода под знаком интеграла к переменной заметим, что при получаем 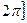, а также

Кроме того, предварительно вычислим

(так что ) и

Получаем:

Делая замену , приходим к интегралу

Дата добавления: 2015-10-30