
|
Читайте также: |
Пусть u и v – две дифференцируемые функции от х. Тогда дифференциал произведения 
Интегрируя, получим 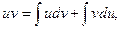 или
или 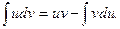
В применении этой формулы и состоит метод интегрирования по частям.
Примеры.
1. 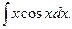
Положим  Тогда
Тогда 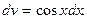 Дифференцируя первое равенство и интегрируя второе имеем:
Дифференцируя первое равенство и интегрируя второе имеем: 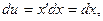
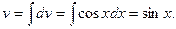 Пользуясь формулой интегрирования по частям, получим:
Пользуясь формулой интегрирования по частям, получим:
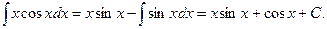
Оформлять эту запись будем так:
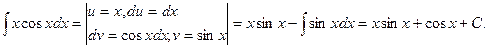
2.

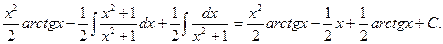
3. 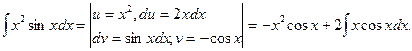
Обратите внимание, что метод интегрирования по частям можно применять несколько раз; при этом важно контролировать, чтобы подынтегральное выражение упрощалось или приводилось к исходному интегралу.
Продолжим решение примера 3. Для второго слагаемого запишем:
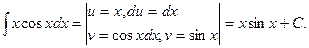
Отсюда
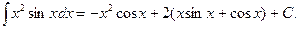
4. 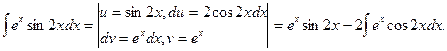
Для второго интеграла еще раз запишем формулу интегрирования по частям:
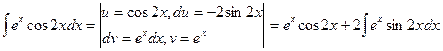
Мы пришли к исходному интегралу. Обозначив его через J, получим равенство:
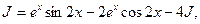 откуда
откуда 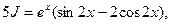


Рекомендация. За u выбирается функция, которая при дифференцировании упрощается, а за dv – оставшееся выражение, содержащее dx, которое легко интегрируется. Отметим, что, выбрав u, мы получим dv автоматически. Если под знаком интеграла стоит произведение логарифмической или обратной тригонометрической функции на алгебраическую, то за u следует принимать функции: arcsin kx, arccos kx, arctg kx, arcctg kx, ln kx (пример 2). Если же под знаком интеграла стоит произведение тригонометрической или показательной функции на алгебраическую, то за u удобно принять алгебраическую функцию.
Если под знаком интеграла стоит произведение sinx или cosx на показательную функцию (пример 4) или тригонометрическая функция от логарифма, то, несколько раз применяя формулу интегрирования по частям, можно получить уравнение относительно искомого интеграла. Такие интегралы называют возвратными.
Найти интегралы.
41. 
42. 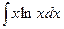
43. 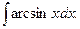
44. 
45. 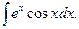
46. 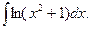
47. 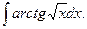
48. 
49. 
50. 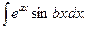
Вопросы и задания для самоконтроля.
1. Докажите, что в методе интегрирования по частям при нахождении функции  мы можем брать любую произвольную константу С, в том числе нуль (в примере 1 v = sinx+C, где С=0, в примере 2 v = - cosx+C, где С=0 и т.д.); для этого в формулу интегрирования по частям подставьте вместо v выражение v+C.
мы можем брать любую произвольную константу С, в том числе нуль (в примере 1 v = sinx+C, где С=0, в примере 2 v = - cosx+C, где С=0 и т.д.); для этого в формулу интегрирования по частям подставьте вместо v выражение v+C.
2. Какие из приведенных ниже интегралов удобно находить методом интегрирования по частям?
а)  б)
б) 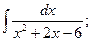 в)
в) 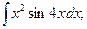 г)
г) 
д) 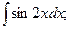 е)
е) 
3. Сформулируйте, в чем состоит метод решения так называемых «возвратных» интегралов?
4. Что следует выбрать в качестве u при нахождении интегралов:
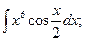

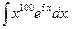
Объясните свой выбор.
Сколько раз придется интегрировать по частям последний из приведенных интегралов?
Дата добавления: 2015-10-30; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод введения новой переменной | | | Интегрирование рациональных функций |