Читайте также:
|
1. Рассмотрим некоторые типы интегралов от тригонометрических функций.
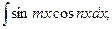
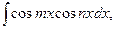
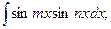
где m,n –постоянные числа.
Здесь применяются формулы:
Примеры.
1. 
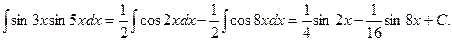
2.
= 
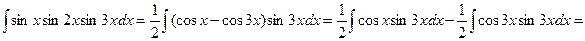
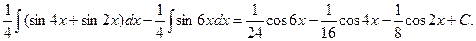
Найти интегралы.
59. 
60. 
61. 
2. 
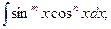где m,n – любые целые показатели.
Пусть один из показателей – нечетное положительное число, например:
n = 2k+1. Положим sinx=t, тогда cosxdx=dt и
Аналогично, если m=2k+1 (т.е. нечетное), t = cosx и т. д.
Примеры.
1. 
Положим sinx = t, тогда cosxdx = dt; получим:
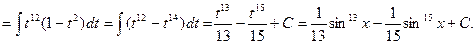
2.
Рекомендация. Если в нечетной степени функция sinx, то обозначать новой переменной следует cosx, а если в нечетной степени cosx, то заменять на sinx.
Если под знаком интеграла стоит произведение четных степеней синуса и косинуса, то, пользуясь формулами:
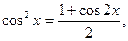
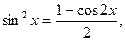
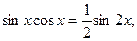
понижают степени синуса и косинуса и затем интегрируют.
Пример.
= 
= 
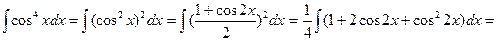
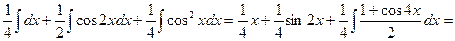
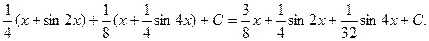
В случае четных степеней часто бывает удобно заменить tg x = t, либо
ctg x = t.
Примеры.
1. 
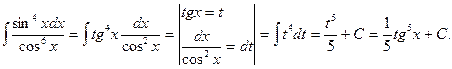
2.
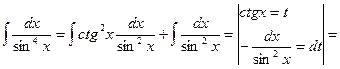
Найти интегралы:
62. 
63. 
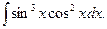
64. 
65. 
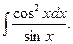
66. 
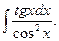
(В №65 помножить числитель и знаменатель на sin x).
3. Интегралы вида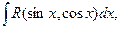 
где R – рациональная функция, сводятся к интегралам от рациональных функций с помощью, так называемой универсальной подстановки: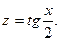 
При этом 
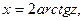
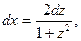
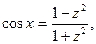
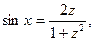
Что следует из известных тригонометрических формул:
и 
.
Пример.
.
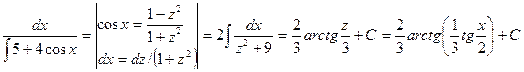Найти интегралы:
67. 
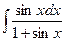. 68. 
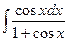. 69.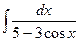 
.
IV. Интегралы вида 
можно вычислить, используя подстановку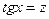 
; при этом 
, 
.
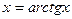Пример
.
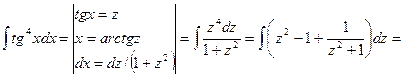
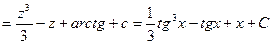Найти интегралы:
70. 
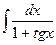, 71.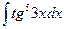 
.
Заметим, что во многих случаях интеграл от тригонометрической функции может быть вычислен в результате применения подходящих преобразований тригонометрических выражений.
Примеры
1. 
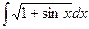, где 
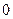<x< 
.
Преобразуем подкоренное выражение, используя формулы
, 
:
.
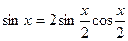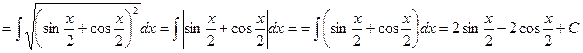(Воспользовались тем, что при 0<x< 
).
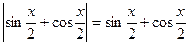2.
.
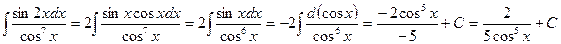Найти интегралы:
72. 
.
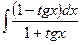73. 
.
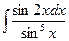74. 
.
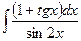75. 
.
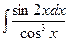76*.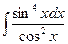 
.
77*.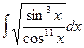 
.
78*.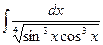 
.
Рассмотренные примеры позволяют сделать вывод: при интегрировании необходимы изобретательность и навыки, приобретаемые практикой решения большого числа примеров.
Вопросы и задания для самопроверки
1. Получите формулы: XVI. 
.
XVII.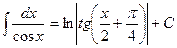 
.
2. Можно ли в случае, когда подстановка cosx=t (или tgx=t) приводит к интегралу от рациональной функции, использовать вместо этих замен подстановку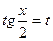 
?
3*. Докажите, что одна из преобразованных четной функции есть функция нечетная, а всякая преобразованная нечетная функция есть функция четная. Приведите примеры.
Дата добавления: 2015-10-30; просмотров: 112 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование рациональных функций | | | Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл |