II. Интегрирование заменой переменной

Одним из основных приемов интегрирования функций является замена переменной (метод подстановки), который состоит в том, что в интеграле , нахождение которого затруднительно, вводят новую переменную , связанную с переменной соотношением

,

где – непрерывная строго монотонная функция, имеющая непрерывную производную 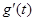на некотором интервале изменения , после чего получают

.

Отметим, что при замене должно осуществляться взаимно однозначное соответствие между областями определения функций , такое, чтобы функция принимала все значения .

Два способа замены переменной

Переменную интегрирования в неопределенном интеграле можно заменить любой непрерывной функцией:

. (I)

Формула (I) определяет собой два способа замены переменной. При чтении формулы слева направо получается способ I:

.

Если будет проще, чем , то эта замена переменной целесообразна. В результате интегрирования получится функция независимой переменной

При чтении справа налево получается способ II:

.

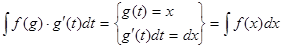Если последний интеграл проще первого, то замена переменной целесообразна.

СПОСОБ I.

.

Общего правила, которое указывало бы, как выбрать функцию , не существует. Умение выбрать эту функцию достигается опытом. Однако для многих типов интегралов подстановка известна и нами будет в соответствующих местах указана. Обратим внимание читателя на то, что, пользуясь подстановкой , надо найти множитель .

Заметим также, что функция должна иметь обратную функцию. Это необходимо для того, чтобы из подстановки можно было определить как функцию .

Задача I.1. Найти интеграл при помощи подстановки .

▲

. ▼

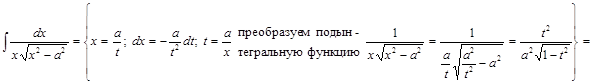
Задача I. 2. Найти интеграл .

▲

. ▼

Задача I. 3. Найти интеграл .

Способ 1.

▲

. ▼

Способ 2.

▲

. ▼

СПОСОБ II.

.

Задача II. 1. Найти интеграл .

▲ . ▼

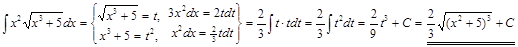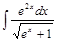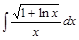Задача II. 2. Найти интегралы: 1) ; 2) ; 3) ; 4) .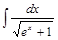

1) ▲

. ▼

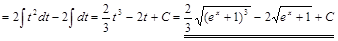2) ▲ . ▼

3) ▲ . ▼

4) ▲

. ▼

ЗАМЕНА ПЕРЕМЕННОЙ В УМЕ

Замена переменной в уме может быть выполнена во втором случае:

,

когда – табличный интеграл, в котором переменная интегрирования 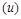– непрерывная функция.

ДЛЯ ИНТЕГРИРОВАНИЯ В УМЕ НЕОБХОДИМО:

Ø ХОРОШО ЗНАТЬ ТАБЛИЧНЫЕ ИНТЕГРАЛЫ И ИХ СТРУКТУРУ,

Ø УМЕТЬ БЫСТРО НАХОДИТЬ ТАБЛИЧНЫЙ ИНТЕГРАЛ, ПОХОЖИЙ НА ДАННЫЙ,

Ø ОВЛАДЕТЬ ПРИЕМОМ ПОДВЕДЕНИЯ ФУНКЦИИ ПОД ЗНАК ДИФФЕРЕНЦИАЛА.

Объясним последнюю операцию:

Подвести функцию под знак дифференциала – значит, проинтегрировать ее в уме и записать под знак дифференциала одну из ее первообразных функций.

Пример 1. Подведите под знак дифференциала следующие функции.

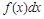
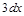
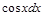
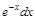
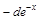
Структура табличных интегралов

Если , то ,

где 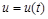– любая непрерывная функция

Пример 2. Посмотрите, как по-разному могут быть записаны табличные интегралы, если воспользоваться формулой 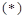при разных функциях :

.

А если записать их иначе:

.

Не правда ли, в интегралах справа очень трудно узнать интеграл, определяющий синус сложной функции.

ИНТЕГРИРОВАНИЕ В УМЕ СОСОТОИТ В ТОМ,

Ø ЧТОБЫ УЗНАТЬ, В КАКОМ ТАБЛИЧНОМ ИНТЕГРАЛЕ, КАКОЙ НЕПРЕРЫВНОЙ ФУНКЦИЕЙ ЗАМЕНЕНА ПЕРЕМЕННАЯ ИНТЕГРИРОВАНИЯ,

Ø ЗАТЕМ ПОДВЕСТИ НУЖНУЮ ЧАСТЬ ПОДЫНТЕГРАЛЬНОЙ ФУНКЦИИ ПОД ЗНАК ДИФФЕРЕНЦИАЛА,

Ø ПОЛУЧИТЬ И ЗАПИСАТЬ ПО ТАБЛИЦЕ СООТВЕТСТВУЮЩЕЕ .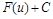

Задача 1. Найти интегралы: 1) ; 2) .

1) ▲ . ▼

2) ▲ . ▼

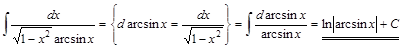Решение задач 1-14 типового варианта

Найти неопределенные интегралы (в задачах 1-5 результаты интегрирования проверить дифференцированием).

1. .

▲

.

Проверим полученный результат:

. ▼

2. .

▲ Способ 1.

.

▲ Способ 2.

.

Проверим полученный результат:

. ▼

3. .

▲ Способ 1.

.

Способ 2.

.

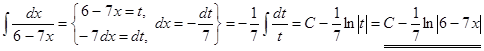Проверим полученный результат:

. ▼

4. .

▲ Способ 1.

.

Способ 2.

.

Проверим полученный результат:

. ▼

5. .

▲ Способ 1.

.

Способ 2.

.

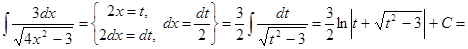
Проверим полученный результат:

. ▼

6. .

▲ Способ 1.

.

Способ 2.

. ▼

7. .

▲ Способ 1.

.

Способ 2.

. ▼

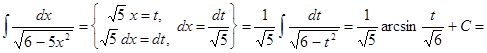
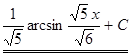8. .

▲ Способ 1.

.

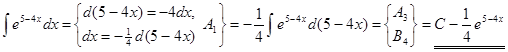Способ 2.

. . ▼

9. .

▲ Способ 1.

.

Способ 2.

. ▼

10. .

▲ Способ 1.

.

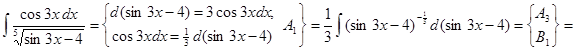
Способ 2.

. ▼

11. .

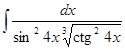▲ Способ 1.

.

Способ 2.

. ▼

12. .

Способ 1.

▲

.

Способ 2.

. ▼

13. .

Способ 1.

▲

.

Способ 2.

. ▼

14. .

▲

. ▼

Дата добавления: 2015-10-30