
|
Читайте также: |
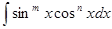 .
.
(Во всем дальнейшем 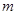 – показатель степени синуса,
– показатель степени синуса, 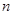 – показатель степени косинуса).
– показатель степени косинуса).
Интегралы этого вида находят с помощью различных тригонометрических формул, применение которых зависит от показателей степеней 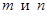 . Рассмотрим наиболее часто встречающиеся случаи
. Рассмотрим наиболее часто встречающиеся случаи
1) Если хотя бы одно из чисел 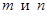 положительно и нечетно, то
положительно и нечетно, то
• от нечетной степени отделяют множитель 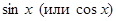 ,
,
• оставшийся множитель в четной степени преобразуют по формуле
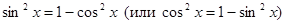 ,
,
• применяют подстановку 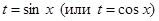 .
.
2) Если оба показателя 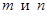 положительны и четны (или один из них – нуль), то показатели степени уменьшают с помощью формул:
положительны и четны (или один из них – нуль), то показатели степени уменьшают с помощью формул:
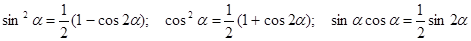 .
.
3) Если 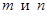 целые отрицательные числа, то интеграл берется непосредственно, если в числителе единицу заменить
целые отрицательные числа, то интеграл берется непосредственно, если в числителе единицу заменить 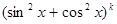 , где
, где 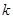 – целая часть числа
– целая часть числа 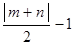 .
.
4) Если 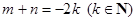 , то подынтегральную функцию
, то подынтегральную функцию
• записывают (или она уже записана) в виде дроби,
• в знаменателе выделяют множитель 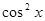 (или
(или 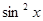 ).
).
• Выражение 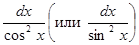 заменяют
заменяют 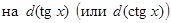 ,
,
• применяют подстановку 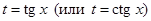 .
.
Задача V.II.1. Найти интегралы: 1) 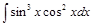 ; 2)
; 2) 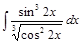 ; 3)
; 3) 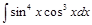 ; 4)
; 4) 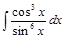 .
.
1) ▲ 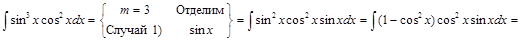
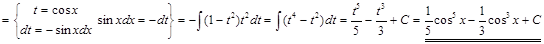 . ▼
. ▼
Замечание. Задачу можно решить, не вводя новую переменную (см. задачу V.I.1)). В дальнейшем поступаем именно так.
2) ▲ 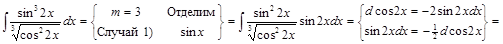
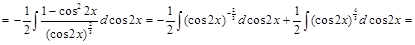
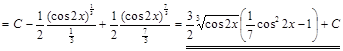 . ▼
. ▼
3) ▲ 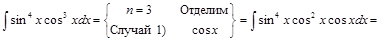
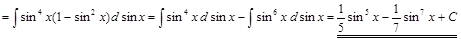 . ▼
. ▼
4) ▲ 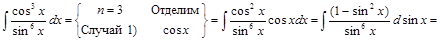
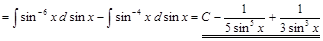 . ▼
. ▼
Задача V.II.2. Найти интегралы: 1) 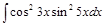 ; 2)
; 2) 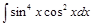 .
.
1) ▲ 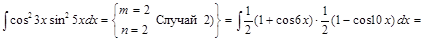
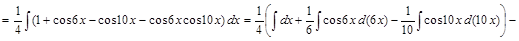
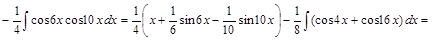
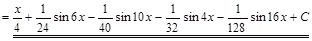 . ▼
. ▼
2) ▲ 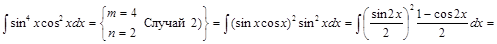
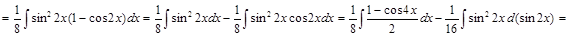
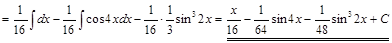 . ▼
. ▼
Задача V.II.3. Найти интеграл 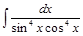 .
.
▲ 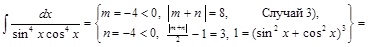
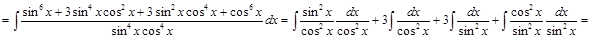
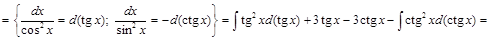
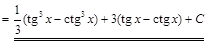 . ▼
. ▼
Задача V.II.4. Найти интегралы: 1) 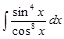 ; 2)
; 2) 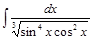 .
.
1) ▲ 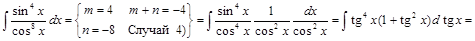
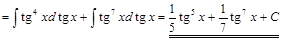 . ▼
. ▼
2) ▲ 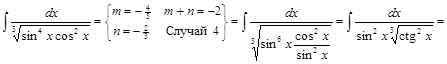
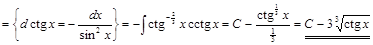 . ▼
. ▼
III. Интегралы вида
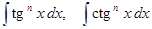 ,
,
где 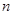 – целое положительное число.
– целое положительное число.
1) К интегралу 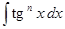 следует применить подстановку
следует применить подстановку 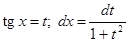 .
.
Получим интеграл 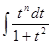 .
.
2) К интегралу 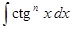 удобно применить подстановку
удобно применить подстановку 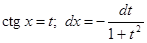 .
.
Получим интеграл 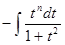 .
.
Выполняя деление, придем к выражению, которое непосредственно интегрируется.
Задача V.III.1. Найти интегралы: 1) 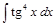 ; 2)
; 2) 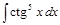 .
.
1) ▲ 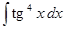
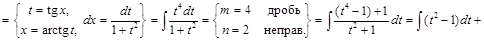
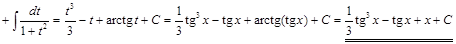 . ▼
. ▼
2) ▲ 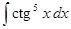
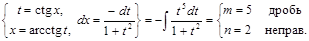
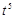
 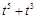
| 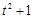
| 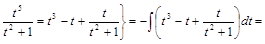
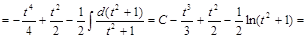
| |
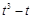
| |||
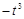
 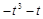
| |||
|
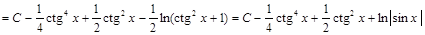 . ▼
. ▼
Замечание. При нахождении интегралов 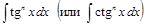 применяется формула
применяется формула
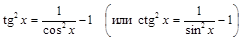 ,
,
с помощью которой последовательно понижается степень тангенса или котангенса.
Задача V.III.1. Найти интегралы: 1) 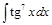 ; 2)
; 2) 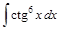 .
.
1) ▲ 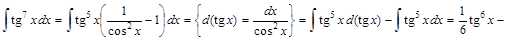
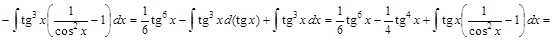
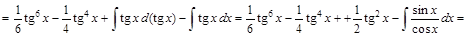
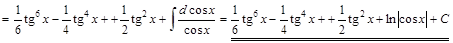 . ▼
. ▼
2) ▲ 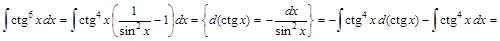
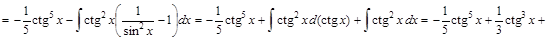
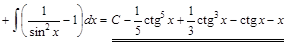 .
.
IV. Интегралы вида
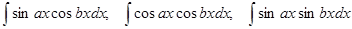 ,
,
где 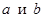 – вещественные числа.
– вещественные числа.
Из тригонометрии известно, что произведения тригонометрических функций, находящихся под знаком этих интегралов, преобразуются в суммы по следующим формулам:
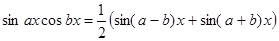 ;
;
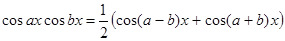 ;
;
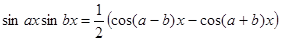 .
.
Заменив в рассматрива6емых интегралах подынтегральные функции по этим формулам, легко выполним интегрирование.
Задача V.IV.1. Найти интегралы: 1) 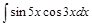 ; 2)
; 2) 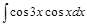 ; 3)
; 3) 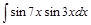 ;
;
4) 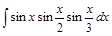 .
.
1) ▲ 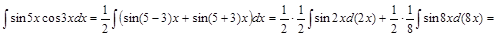
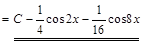 . ▼
. ▼
2) ▲ 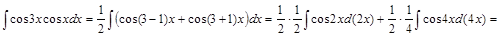
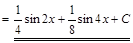 . ▼
. ▼
3) ▲ 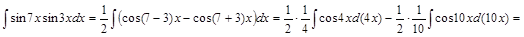
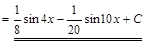 . ▼
. ▼
4) ▲ 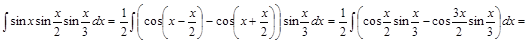
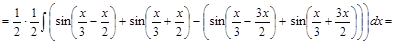
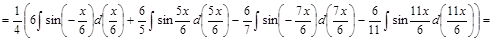
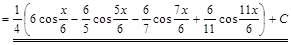 . ▼
. ▼
Дата добавления: 2015-10-30; просмотров: 140 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование простейших дробей | | | V. Интегралы вида |