Знания и умения, которыми должен владеть студент

Знания на уровне понятий, определений, описаний, формулировок

1. Первообразная.

2. Неопределенный интеграл, свойства.

3. Таблица неопределенных интегралов.

4. Интегрирование функций, содержащих квадратный трехчлен.

5. Интегрирование по частям. Некоторые классы функций, интегрируемых по частям.

6. Интегрирование простейших элементарных дробей.

7. Интегрирование рациональных дробей.

8. Интегрирование функций .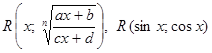

9^*. Интеграл от дифференциального бинома.

10. Определение неберущегося интеграла. Примеры.

Знания на уровне доказательств и выводов

1. Свойства неопределенного интеграла.

2. Теорема о замене переменной.

3. Формула интегрирования по частям.

Умения в решении задач

Студент должен уметь:

1. Сводить интегралы к табличным.

2. Подбирать нужную замену переменной в интегралах известных типов.

3. Интегрировать простейшие рациональные и иррациональные выражения, содержащие квадратный трехчлен.

4. Интегрировать по частям. Знать классы функций, интегрируемых по частям.

5. Интегрировать рациональные дроби.

6. Сводить интегралы от некоторых иррациональных выражений к интегралам от рациональных функций.

7. Интегрировать простейшие тригонометрические функции и функции вида .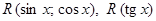

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

1. Козлов В. Н., Максимов Ю. Д., Хватов Ю. А. Структурированная программа (базис). Типовые задачи для контроля, требования к знаниям и умениям студентов. Учебное пособие. – СПб.: СПБГТУ, 2001. – 56 с.

2. Краснов М. Л. и др. Вся высшая математика: Учебник. Т. 1, 2. – М.: Эдиториал УРСС, 2000. – 328 с.

3. Зорич В. А. Математический анализ, часть 1. – М.: Наука, 1981. – 544 с.

4. Веретенников В. Н. Математический анализ: Учебное пособие (рукопись). – СПб.: РГГМУ, 2006.

5. Рябушко А. П. и др. Сб. индивидуальных заданий по высшей математике: Учебное пособие. Ч. 1. – Мн.: Выш. шк., 1990. – 270 с.

6. Виноградова И. А., Олехник С. Н., Садовничий В. А. Задачи и упражнения по математическому анализу. В 2 кн. – М.: Высш. шк., 2000.

7. Кузнецов Л. А. Сборник задач по высшей математике (типовые расчеты). – М.: Высш. шк., 1986.

СОДЕРЖАНИЕ

Стр.

1. Предисловие …………………………………………………………………………… 3

2. Основные приемы и методы интегрирования ……………………………………… 4

3. Непосредственное интегрирование ……………………………………… ………… 5

4. Интегрирование заменой переменной ……………………………………………… 14

Решение задач 1-14 типового варианта …………………………………………… 17

5. Интегрирование по частям …………………………………………………………… 22

Решение задач 15-18 типового варианта ………………………………………… 26

6. Интегрирование рациональных функций …………………………………………… 27

Решение задач 19-21 типового варианта ………………………………………… 36

7. Интегрирование выражений, содержащих тригонометрические функции ……… 38

Решение задач 22-24,26 типового варианта ……………………………………… 45

8. Интегрирование некоторых иррациональных функций …………………………… 46

Решение задач 27, 28, 25 типового варианта ……………………………………… 52

9. Интегрирование разных функций …………………………………………………… 53

10. Знания и умения, которыми должен владеть студент ……………………………… 55

11. Использованная литература …………………………………………………………… 55

Учебное издание

Дата добавления: 2015-10-30