Краткие сведения о рациональных функциях

Простейшей рациональной функцией является многочлен степени, т. е. функция вида

, (IV.1)

где – вещественные постоянные, причем . Многочлен , у которого коэффициент , называется приведенным.

Корни многочлена.

Вещественное число называется корнем многочлена , если .

Разложение многочлена на множители.

1. Если числа являются корнями многочлена , то этот многочлен может быть разложен на множители по формуле

. (IV.2)

2. Многочлен степени не может иметь больше, чем различных корней.

3. Корень многочлена называется простым, если в разложение (IV.2) множитель входит один раз.

Если же этот множитель в формулу (IV.2) входит раз, то корень называется корнем кратности многочлена (IV.1).

4. Если многочлен (IV.1) имеет не только вещественные, но и комплексные корни, то вместо формулы (IV.2) имеет место формула

(IV.1),

где 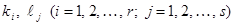– натуральные числа.

Квадратичные множители , входящие в эту формулу, не имеют вещественных корней и на множители первой степени с вещественными коэффициентами не разлагаются (здесь – вещественные коэффициенты).

Рациональная дробь.

Рациональной функцией 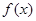или рациональной дробью называется отношение двух многочленов

,

причем предполагается, что многочлены не имеют общих множителей.

Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе, т. е. .

Если же 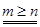, то рациональная дробь называется неправильной, ее можно представить в виде

,

где – некоторые многочлены, а является правильной рациональной дробью.

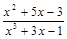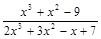Пример IV. 1. 1) ; 2) ; 3) .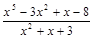

1) ▲ . Дробь правильная (степень числителя меньше степени знаменателя). ▼

2) ▲ . Дробь неправильная (степень числителя равна степени знаменателя). ▼

3) ▲ . Дробь неправильная (степень числителя больше степени знаменателя). ▼

Из неправильной рациональной дроби всегда можно выделить целую часть (многочлен). Это достигается делением числителя на знаменатель по правилу деления многочленов.

Пример IV. 2. Рациональная функция является неправильной дробью.

▲ Разделив на «уголком», будем иметь

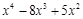
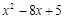
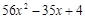
и, таким образом,

. ▼

Простейшие дроби.

Определение. Простейшими (или элементарными) дробями называются рациональные дроби следующих четырех типов:

I. ; II. ; III. ; IV. ,

Где – вещественные числа, – натуральное число, большее или равное 2, а квадратный трехчлен не имеет вещественных корней, так что его дискриминант .

Разложение рациональной дроби на простейшие.

В алгебре доказывается теорема.

Теорема IV.1. Правильная рациональная дробь с вещественными коэффициентами, знаменатель которой 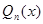имеет вид

,

разлагается единственным способом на сумму простейших дробей по правилу

,

где 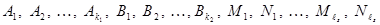– вещественные числа, подлежащие определению.

Дата добавления: 2015-10-30