Интегрирование простейших дробей. Как было сказано выше, любую неправильную рациональную дробь можно представить в виде

Как было сказано выше, любую неправильную рациональную дробь можно представить в виде суммы некоторого многочлена и правильной рациональной дроби, причем это представление единственно.

Целая рациональная функция (многочлен) интегрируется непосредственно:

.

Так как любая правильная рациональная дробь представима в виде суммы простейших дробей, то ее интегрирование сводится к интегрированию простейших дробей. Рассмотрим вопрос об их интегрировании.

I. .

Задача IV.5. Найти интегралы: 1) ; 2) ; 3) ; 4) .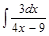

1) ▲ . ▼

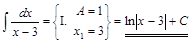2) ▲ . ▼

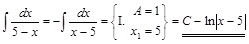3) ▲ . ▼

4) ▲ . ▼

II. .

Задача IV.6. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲ . ▼

2) ▲ . ▼

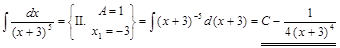3) ▲ . ▼

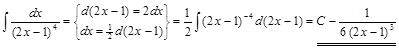4) ▲ . ▼

Интегрирование дробей первых двух типов очевидно. Такие дроби дальше нужно интегрировать в уме.

III. .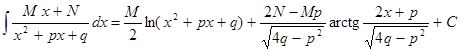

1. Прием выделения полного квадрата из квадратного трехчлена.

.

Так как второе слагаемое , то положим его равным 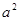, где , а затем сделаем подстановку . Тогда, учитывая линейные свойства интеграла, найдем:

.

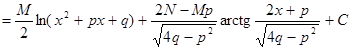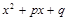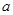Замечание. Если в знаменателе дроби вместо квадратичного трехчлена находится трехчлен , то коэффициент следует вынести за скобку и тем самым свести этот случай к предыдущему.

Задача IV.7. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲

. ▼

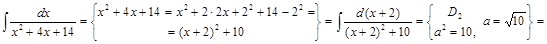
2) ▲

. ▼

3) ▲

. ▼

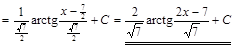4) Эта задача отличается от предыдущих задач тем, что коэффициент 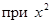в знаменателе не равен единице. Для того чтобы свести этот случай к предыдущим, будем это коэффициент выносить за скобку.

▲

. ▼

Задача IV.8. Найти интеграл

▲

. ▼

2. Прием выделения одной линейной функции из другой.

Для вычисления интеграла 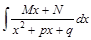можно поступать так:

Ø в числителе подынтегральной дроби записывается производная знаменателя, т. е.

.

Тождественными преобразованиями получают заданный числитель .

Для этого следует двучлен 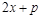умножить и к полученному произведению прибавить . Очевидно, что

.

Ø Преобразованная дробь имеет вид

и может быть представлена как сумма двух дробей:

.

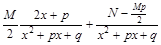Первая дробь интегрируется просто: в числителе находится производная знаменателя – интегрирование приводит к натуральному логарифму модуля знаменателя.

Для интегрирования второй дроби в знаменателе выделяют полный квадрат.

Задача IV.9. Найти интеграл .

▲

. ▼

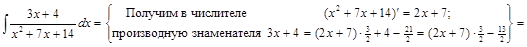
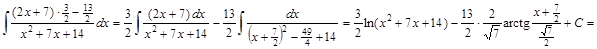
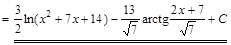Замечание. Под знаком логарифма трехчлен не взят по абсолютной величине, так как дискриминант отрицателен, а поэтому при любом значении этот трехчлен положителен.

IV. .

Для нахождения интеграла от простейшей дроби четвертого типа положим, как и выше,

.

Тогда получим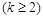

.

Обозначая интеграл в правой части , после преобразований имеем

.

Имеем так называемую рекуррентную формулу, которая позволяет найти интеграл для любого .

Задача IV.10. Найти интеграл .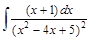

▲ .

Полагая в рекуррентной формуле , будем иметь

,

и, следовательно, искомый интеграл равен

.

Общий случай

Для нахождения неопределенного интеграла от дробно-рациональной функции следует поступать следующим образом:

Если рациональная дробь неправильная, то делением числителя на знаменатель выделяется целая часть, т. е данная функция представляется в виде суммы многочлена и правильной рациональной дроби;

Дата добавления: 2015-10-30