Интегрирование по частям

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Первообразная, основное свойство первообразных

Определение. Первообразной функции называется функция , производная которой равна , т.е. .

Поскольку , где постоянная, первообразных функции бесчисленное множество.

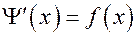Теорема. Любые две первообразные функции могут отличаться только на постоянную. Другими словами, если и , то

Доказательство: Обозначим Согласно предположению Следовательно, имеем:

.

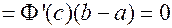
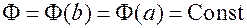Определение. Множество всех первообразных одной функции называется неопределенным интегралом этой функции и обозначается , причем называется подынтегральной функцией, подынтегральным выражением.

Очевидно, что если , то , где произвольная постоянная интегрирования, то есть постоянная может принимать любые значения.

Приведем таблицу неопределенных интегралов с проверкой того, что действительно производная от правой части совпадает с подынтегральной функцией.

Таблица неопределенных интегралов

1.	.
2.
3.	.
4. .
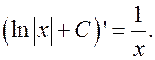
5. .	.
6.
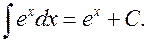
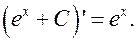
7.
8. .
9.
10. .
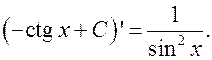
11.
12.
13.
14.
15.
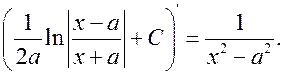
16.
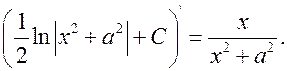
17. .
18.

Приемы интегрирования

Тождественные преобразования подынтегрального выражения и использование свойств интегралов

(непосредственное интегрирование).

Из свойства производной

следует аналогичное свойство для неопределенных интегралов

.

Пример 1.

Пример 2.

Замена переменной в интеграле

Докажем, что если 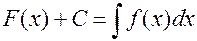, то .

Доказательство: Имеем: 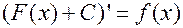. Тогда

.

Формула интегрирования заменой переменной:

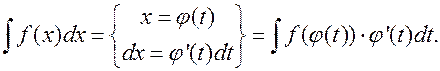
После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования назад к старой переменной .

При подходящей замене переменной мы сводим заданный интеграл к табличному.

Пример 1.

Пример 2.

.

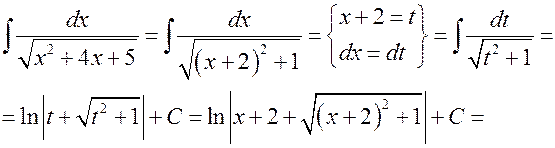
Пример 3.

Интегрирование по частям

Пусть , – функции, имеющие непрерывные производные. Тогда

(или ).

Доказательство: Справедливы соотношения:

и

Сравнивая правые части, получим приведенную выше формулу.

Можно указать приоритеты выбора функции .

1) В качестве выбирается одна из функций , .

2) При отсутствии этих функций в подынтегральном выражении в качестве может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.

Других приоритетов при выборе этой функции нет, выбор в этом случае осуществляется перебором возможных вариантов.

Пример 1.

Пример 2.

Дата добавления: 2015-10-30