
|
Читайте также: |
 1. Множество первообразных функции
1. Множество первообразных функции  имеет вид:
имеет вид:
А)  +С
+С  Б)
Б)  +С В)
+С В)  +С Г)
+С Г)  +С
+С
2. Множество первообразных функции 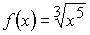 имеет вид:
имеет вид:
А)  Б)
Б)  В)
В)  Г)
Г) 
3. Множество первообразных функции  имеет вид:
имеет вид:
А)  Б)
Б) 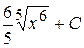 В)
В)  Г)
Г) 
4. Множество первообразных функции  имеет вид:
имеет вид:
А)  +С Б)
+С Б)  +С В)
+С В) 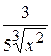 +С Г)
+С Г) 
 +С
+С
5. Множество первообразных функции  имеет вид:
имеет вид:
А) 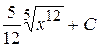 Б)
Б)  В)
В)  Г)
Г) 
6. Множество первообразных функции  имеет вид:
имеет вид:
А)  Б)
Б) 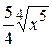 +С В)
+С В) 
 Г)
Г)  +С
+С
7. Множество первообразных функции  имеет вид:
имеет вид:
А)  Б)
Б)  + С В)
+ С В)  + С Г)
+ С Г) 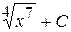
8. Множество первообразных функции  имеет вид:
имеет вид:
А) 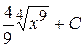 Б)
Б)  В)
В) 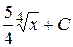 Г)
Г) 
9. Множество первообразных функции  имеет вид:
имеет вид:
А)  Б)
Б)  В)
В) 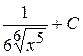 Г)
Г) 
10. Множество первообразных функции 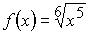 имеет вид:
имеет вид:
А) 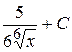 Б)
Б) 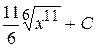 В)
В)  Г)
Г) 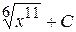
11. Множество первообразных функции  имеет вид:
имеет вид:
А)  +С Б)
+С Б)  В)
В)  Г)
Г) 
12. Множество первообразных функции  имеет вид:
имеет вид:
А)  Б)
Б) 
В)  Г)
Г) 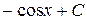
13. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б)  В)
В)  Г)
Г) 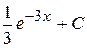
14. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 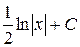 Б)
Б)  В)
В)  Г)
Г) 
15. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б)  В)
В)  Г)
Г) 
16. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 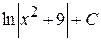 Б)
Б)  В)
В)  Г)
Г) 
17. Множество первообразных функции f(x) = 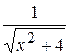 имеет вид:
имеет вид:
А)  Б)
Б) 
В) 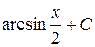 Г)
Г) 
18. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 
В)  Г)
Г) 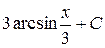
19. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 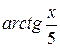 Б)
Б) 
В)  Г)
Г) 
20. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б)  В)
В) 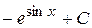 Г)
Г) 
21. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 
В) 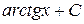 Г)
Г) 
22. Множество первообразных функции f(x) = 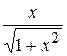 имеет вид:
имеет вид:
А) 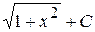 Б)
Б) 
В)  Г)
Г) 
23. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 
В) 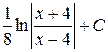 Г)
Г) 
24. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 
В)  Г)
Г) 
25. Вычислить неопределенный интеграл от функции f(x) =  :
:
А) 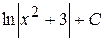 Б)
Б) 
В)  Г)
Г) 
26. Вычислить неопределенный интеграл от функции f(x) =  :
:
А)  Б)
Б) 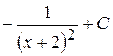
В)  Г)
Г) 
27. Множество первообразных функции f(x) = 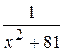 имеет вид:
имеет вид:
А)  Б)
Б) 
В) 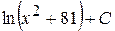 Г)
Г) 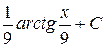

28. Множество первообразных функции f(x) = 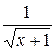 имеет вид:
имеет вид:
А)  Б)
Б) 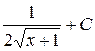
В)  Г)
Г) 
29. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 
В)  Г)
Г) 
30. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 
В)  Г)
Г) 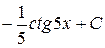
31. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б)
Б) 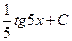
В) 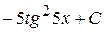 Г)
Г) 
32. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А) 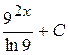 Б)
Б)  В)
В)  Г)
Г) 
33. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  Б) 7
Б) 7  + С В)
+ С В)  + С Г)
+ С Г) 
34. Множество первообразных функции f(x) =  имеет вид:
имеет вид:
А)  + С Б)
+ С Б)  + С
+ С
В)  + С Г)
+ С Г) 
35. Множество первообразных функции f(x) = 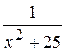 имеет вид:
имеет вид:
А)  Б)
Б) 
В)  Г)
Г) 
36. Функция F(x) называется первообразной функции f (x) на интервале (а,b), если для любого  выполняется равенство
выполняется равенство
А) 
Б) 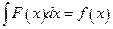
+ В) 
Г) 
37.Дифференциал от неопределенного интеграла равен 
А) 
+ Б)  dx
dx
В) 
Г) 
38. Производная неопределенного интеграла равна 
+ А) 
Б)  dx
dx
В) 
Г) 
39. Неопределенный интеграл от дифференциала некоторой функции равен 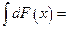
А) 
Б)  dx
dx
В) 
+ Г) 
40. Пусть а- постоянная величина тогда 
А) 
Б) 
+ В) 
Г) 
41. 
А) 
+ Б) 
В) 
Г) 
42. Формула интегрирования по частям имеет вид:
+ А) 
Б) 
В) 
Г) 
43. Пусть требуется вычислить интеграл 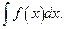 Сделаем подстановку
Сделаем подстановку  где
где  - функция, имеющая непрерывную производную. Тогда формула замены переменных в неопределенном интеграле имеет вид:
- функция, имеющая непрерывную производную. Тогда формула замены переменных в неопределенном интеграле имеет вид:
А) 
Б) 
В) 
+ Г) 
44. Функция вида: 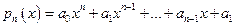 , где n – натуральное число,
, где n – натуральное число,  - постоянные коэффициенты, называется
- постоянные коэффициенты, называется
+ А) целой рациональной функцией;
Б) дробно-рациональной функцией
В) иррациональной функцией
Г) рациональной дробью
45. Корнем многочлена  называется такое значение x0 переменной x, при котором
называется такое значение x0 переменной x, при котором
+ А) 
Б) 
В) 
Г) 
46. Если x 1, x 2,….. x n- корни многочлена P n(x), а 0 – коэффициент многочлена при x n, то многочлен P n(x) можно представить в виде:
А) P n(x0) = 0
+ Б) P n(x) = а 0 (x – x 1)(x – x 2)…….(x - x n)
В) P n(x) = а 0 (x + x 1)(x + x 2)…….(x + x n)
Г) P n(x) = (x - x 1)(x - x 2)…….(x - x n)
47. Если x 1 – корень многочлена P n(x) кратности k1, x 2 – кратности k2, …, корень xr имеет кратность kr, при этом k1 + k2 +….+ kr = n, а 0 – коэффициент при x n разложение многочлена P n(x) можно записать в виде:
А) P n(x) = а 0 (x + x 1)(x + x 2)…….(x + x r)
Б) P n(x) = (x - x 1)(x - x 2)…….(x - x r)
+ В) P n(x) = а 0 (x – x 1) 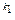 (x – x 2)
(x – x 2)  …….(x - x n)
…….(x - x n) 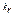
Г) P n(x) = а 0 (x + x 1) 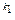 (x + x 2)
(x + x 2)  …….(x + x n)
…….(x + x n) 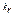
48. Рациональная дробь называется правильной, если
А) степень числителя равна степени знаменателя
+ Б) степень числителя меньше степени знаменателя
В) степень числителя больше степени знаменателя
Г) степень числителя и степени знаменателя равны единице
49. 
+ А) 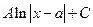
Б) 
В) 
Г) 
50. 
А) 
Б) 
В) 
+ Г) 
51. Непрерывная функция имеет
А) только одну первообразную
+ Б) бесконечное множество первообразных
В) две первообразных
52. Две различные первообразные одной и той же функции
А) равны между собой
+ Б) отличаются на константу
В) отличаются на некоторую функцию
53. К интегрируемым функциям относятся все
А) постоянные
+ Б) непрерывные
В) прерывные
54. Совокупность всех первообразных  от функции f(x) называется
от функции f(x) называется
А) дифференциалом 
Б) определенным интегралом
+ В) неопределенным интегралом
55. Проверить соответствие формул:
1)  ; 2)
; 2)  ; 3)
; 3) 
+ А) верно
Б) ошибка в 2)
В) ошибка в 3)
Дата добавления: 2015-10-30; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование по частям | | | Определенный интеграл |