Вычисление двойного интеграла

Сводится к последовательному вычислению двух определённых интегралов.

1) Случай прямоугольной области. Пусть область образована прямыми и описывается системой неравенств 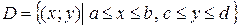. Если функция непрерывна в D, то существует двойной интеграл

. (5)

Интеграл в правой части равенства (5) называется повторным интегралом, в нём интегралы и называются соответственно внешним и внутренним интегралами, переменные и – соответственно внешней и внутренней переменными интегрирования.

Если взять за внешнюю переменную, а – за внутреннюю, то имеем аналогичную формулу

. (6)

Формулы (5) и (6) обычно записывают, не употребляя скобок:

.

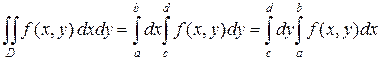2) Случай криволинейной области специального вида («правильной» области).

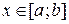а) пусть D – область, ограниченная прямыми и непрерывными кривыми , так что для всех выполнено неравенство (см. рисунок). Тогда область , причём любая прямая , параллельная оси Оу, пересекает границу не более двух раз. Такую область будем называть «правильной в направлении оси Оу». Тогда

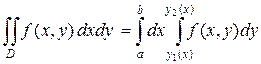. (7)

б) если область ограничена линиями , , , , где 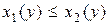для всех , т.е. определяется системой неравенств (см. рисунок), то любая прямая , параллельная оси Ох, пересекает границу D не более двух раз. Такую область назовём «правильной в направлении оси Ох» и будем иметь тогда

. (8)

Пример 1. Область определяется неравенствами , , 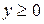. Перейти в двойном интеграле к повторному интегралу двумя способами.

Перейдём вначале к повторному интегралу вида (7). Как следует из рисунка, в точках области выполняется неравенство . При любом таком прямая, параллельная оси Оу, пересекает , входя в неё через прямую и выходя через верхнюю полуокружность . Поэтому значение внутренней переменной меняется от 0 до , и интеграл .

При способе (8) выбора переменных имеем аналогично , и .

3) Вычисление двойного интеграла в общем случае.

Область интегрирования может быть такой, что:

- прямые, параллельные осям координат, в некоторых случаях пересекают более чем в двух точках (см. рисунок);

- граница составная, то есть состоит из нескольких разных линий (см. рисунок).

В таких случаях область разбивают на «правильные» криволинейные области инаходят двойные интегралы по этим областям. Интеграл по всей области определяется тогда согласно свойству 3 (аддитивность) как сумма найденных интегралов.

Дата добавления: 2015-10-30