Криволинейные координаты на плоскости

Пусть непрерывные однозначные функции

(9)

ставят в соответствие каждой точке области на плоскости одну определённую точку некоторой области плоскости . Если отображение (9) взаимнооднозначное, т.е. разным точкам из соответствуют разные точки из , то существуют обратные функции

. (10)

Если функции (9) непрерывны и имеют непрерывные частные производные первого порядка, то определитель всюду в области отличен от нуля. Этот функциональный определитель называется определителем Якóби или, коротко, якобианом системы функций (10).

Переменные u, v определяют не только положение точки 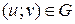на плоскости , но и положение точки , находящейся с во взаимнооднозначном соответствии. Тем самым числа u и v можно рассматривать как новые координаты точки в области .

Координатной линией (в некоторой системе координат) называют кривую, вдоль которой одна из координат сохраняет постоянное значение. Так, прямые 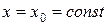и являются координатными линиями в прямоугольной системе координат, образуя на плоскости прямоугольную сеть. При этом каждая точка плоскости является точкой пересечения двух координатных прямых – по одной из каждого семейства и .

Положим теперь в (10) . Полученные уравнения , 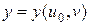являются параметрическими уравнениями некоторой кривой в области , вдоль которой изменяется только v. Точно так же, положив в (10) , получим , – параметрические уравнения кривой в области , вдоль которой изменяется только u. Таким образом, в области плоскости наряду с обычной сеткой прямоугольных координат возникает новая координатная сетка, образованная кривыми и . Поэтому числа u и v принято называть криволинейными координатами точки. Каждая точка является точкой пересечения двух координатных линий – по одной из каждого семейства и .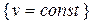

Пример 2 (полярные координаты на плоскости).

Полярная система координат является наиболее часто используемой криволинейной системой координат на плоскости. На плоскости задаётся точка О, называемая полюсом, и луч с началом в полюсе, называемый полярной осью. Положение точки М определяется тогда длиной радиус-вектора точки и углом между радиус-вектором и полярной осью, с положительным направлением отсчёта против хода часовой стрелки. Величина называется полярным радиусом точки, величина – полярным углом.

Если на плоскости уже задана прямоугольная система координат , то в качестве полюса обычно выбирают начало координат , а в качестве полярной оси – ось 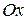(см. рис.). Связь введённых таким образом полярных координат с декартовыми координатами осуществляется по формулам

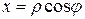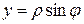, , (11)

где , (или ).

Координатными линиями в полярной системе координат служат концентрические окружности с центром в полюсе и лучи , «веером» расходящиеся из полюса.

Якобиан преобразования (11)

.

Дата добавления: 2015-10-30