Декартовы прямоугольные координаты в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении.

- формула для определения расстояния между двумя точками и

Координаты х, у, z точки М, которая делит отрезок , ограниченный точками и , в отношении , определяются по формулам:

, ,

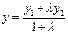В частности, при l = 1 имеем координаты середины данного отрезка:

_{, ,}

Задача 1. Пусть в данной системе координат даны точки A(1,2,3) и B(5,4,3). Найти координаты т.С, т.ч. АВ=2АС.

Пусть координатам точки А (a,b,c) соответствуют А (1,2,3), a B(d,e,f) - В (5,4,3).

Ввести в диалоговое окно формулу для вычисления координаты х=(а+d)/2 и нажать

В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения а=1; d=-5 и нажать кнопку . Получили координату х точки С: х=-3

Аналогично находят координату «у» точки С по формуле y=(b+e)/2, и координату «z» по формуле z=(c+f)/2.

Задача 2. Найти расстояние между точками А(-2,1,3) и В(0,-1,2). [Цубербиллер, Гл.7,№711]

Ввести формулу для вычисления расстояния между двумя точками =((d-а)^2+(e-b)^2+(f-с)^2)^(1/2) в строку ввода диалогового окна Autor Expression и нажать , для вывода формулы в рабочее окно программы.

В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения и нажать кнопку . Получили искомое расстояние: .

Задача 3. Доказать, что треугольник с вершинами А₁ (3; — 1; 6), А₂ (—1; 7; —2) и А₃ (1; —3; 2) прямоугольный. [Клетеник, № 729]

Ввести формулу для вычисления расстояния между двумя точками =((d-а)^2+(e-b)^2+(а-с)^2)^(1/2) в строку ввода диалогового окна Autor Expression и нажать , для вывода формулы в рабочее окно программы.

В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения и нажать кнопку . Получили расстояние между двумя точками, т.е. длину одной стороны.

Аналогично, находим длины двух других сторон.

Сравнивая длины, по теореме Пифагора доказываем, что треугольник прямоугольный.

Задача 4. На оси z найти точку, равноудаленную от точек: А(-4,1,7) и В(3,5,2). [Цубербиллер, Гл.7, №714]

Пусть (0,0,z) - искомая точка. Приравнивая расстояния от нее до данных точек, получим:

или .

Ввести в диалоговое окно 17+(z-7)^2=34+(z+2)^2 и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Чтобы найти приближенное значение полученного выражения в меню Simplifyвыбрать подменю . В появившемся диалоговом окне задать количество цифр после запятой и нажать кнопку .

Дата добавления: 2015-10-23