Уравнение цилиндрической поверхности с образующими, параллельными одной из координатных осей.

- уравнение поверхности с тремя переменными.

Линия в пространстве определяется совместным заданием двух урав­нений

.

Каноническое уравнение конуса: .

Цилиндры второго порядка определяются уравнениями:

(эллиптический цилиндр, в частности при a = b круговой);

(гиперболический цилиндр);

(параболический цилиндр).

Задача 1. Найти точки пересечения трёх поверхностей:

, , .

В меню Solve выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения x^2+y^2+z^2=9, x^2+y^2+(z-2)^2 =5 и y-2=0.

Нажать кнопку . Получим два решения, следовательно две точки пересечения с соответствующими координатами.

Задача 2. Составить уравнение цилиндрической поверхности, если известно уравнение ее оси и координаты одной из ее точек .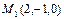

Анализ: Направляющий вектор оси , точка оси . Вектор . Площадь параллелограмма, построенного на векторах р и а вычисляется по формуле , с другой стороны .

Определим данные вектора: р:=[3,4,2], а:=[-5,-2,-3].

Найдем скалярное произведение векторов.. Для этого ввести в диалоговое окно выражение cross(р,а) и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Найдем модуль векторного найденного произведения и модуль вектора р. Для этого ввести в диалоговое окно формулу для вычисления модуля вектора (b^2 + c^2 + d^2)^(1/2) и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения координат векторного произведения и нажать кнопку . Получим . Аналогично находим модуль вектора р, предварительно выделив в активном окне формулу для нахождения модуля вектора. Получим

Используя формулу для вычисления площади параллелограмма построенного на векторах, находим h – расстояние от оси, на котором находятся все точки цилиндрической поверхности. Для этого ввести в диалоговое окно 3·√29/√29 и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Определить вектор . И найти векторное произведение .

Найти модуль данного векторного произведения, приравнять его к нулю.

Упростить данное выражение можно: в меню выбрать подменю , убрать в появившемся окне выделение с переменных и нажать .

Получим искомое уравнение цилиндрической поверхности.

Дата добавления: 2015-10-23