Глава 2. Уравнение линии

Функция двух переменных.

Понятие уравнения линии. Задание линии при помощи уравнения.

Вывод уравнений заранее данных линий.

Параметрические уравнения линии.

- уравнение с двумя переменными.

- параметрическое уравнение с двумя переменными.

Задача 1. Даны линии:1) х + у = 0; 2) x ² + y ² — 36 = 0. Определить, какие из них проходят через начало координат. (Клетеник, №160 (п.1,3))

Ввести в диалоговое окно выражениех + у = 0 и нажать

В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения x=0; y=-0 и нажать кнопку . Получили верное равенство 0=0. Следовательно, линия х + у = 0 проходит через начало координат.

Аналогично проверяют, проходит ли вторая линия через начало координат.

Задача 2. В полярной системе координат даны точки М₁ (1; 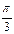), М₂ (2;0), М₃ (2; ), М₄ (; ) и М₅ (1; ). Установить, какие из этих точек лежат на линии, определённой уравнением в полярных координатах r = 2 cos q, и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить её на чертеже) (Клетеник, №163)

Ввести в диалоговое окно выражениеr=2cos(q) и нажать

В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения ρ=1; θ=-π/3 и нажать кнопку . Получили верное равенство 1=1. Следовательно, данная точка лежит на линии r=2cos(q).

Аналогично проверяют все остальные точки. Получим, точки М₁, М₂, М₄ принадлежат данной линии, а точки М₃ и М₅ не принадлежат.

Задачи для самостоятельного решения:

Даны линии:1) х — у = 0; 2) x ²+ y ²—2 x ==0; 3) x ²+ y ²+ 4 x —6 y —1 =0.

Определить, какие из них проходят через начало координат. [Клетеник, №160, п.2,4,5]

[1 и 2 проходят через начало координат]

Даны линии:

1) x ² + y ² = 49; 2) (x — 3)² + (y + 4)² = 25;

3) (x + 6)² + (y — 3)² = 25; 4) (x+ 5)² + (y — 4)² = 9;

5) x ² + y ²— 12 х + 16 у = 0; 6) x ² + y ² — 2 х + 8 у + 7 = 0;

7) x ² + y ² — 6 х + 4 у + 12 = 0. Найти точки их пересечения: а) с осью Ох; б) с осью Оу. [Клетеник, №161]

[1) а) (7; 0), (–7; 0); б) (0; 7), (0; –7);

2) а) (0; 0), (6; 0); б) (0; 0), (0; –8);

3) а)(– 10; 0), (— 2; 0); б) линия с осью Оу не пересекается;

4) линия с координатными осями не пересекается;

5) а) (0; 0), (12; 0); б) (0; 0), (0; –16);

6) а) линия с осью Ох не пересекается; б) (0; –1), (0; –7);

7) линия с координатны­ми осями не пересекается.]

Найти точки пересечения двух линий;

1) х ² +у ² = 8, х—у = 0;

2) х ² +у ²—16 x +4 у +18 = 0, х + у = 0;

3) х ² +у ²—2 x +4 у —3 = 0, х ² + у ²= 25;

4) х ² +у ²—8 x +10у+40 = 0, х ² + у ²= 4. [Клетеник, №162]

[1) (2; 2), (- 2; - 2);

2) (1; -1), (9; - 9);

3) (3; -4), (1 ; -4 );

4) линии не пересекаются.]

Дата добавления: 2015-10-23