Преобразование координат.

, – декартовы прямоугольные координаты произвольной точки М.

, - формулы перехода от полярных координат произвольной точки к декартовым координатам той же точки.[*]

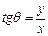, - формулы перехода от декартовых координат произвольной точки к полярным координатам той же точки.*

- формула нахождения расстояния между двумя точками в прямоугольной декартовой системе координат.

- формула нахождения расстояния между двумя точками в полярной системе координат.

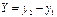, - формулы проекции на оси координат направленного отрезка М₁М₂, где М₁(х₁;у₁) и М₂(х₂; у₂).

, - формулы проекции произвольного отрезка на координатные оси через его длину и полярный угол.

, - формулы координат точки М, проходящей через данные точки М₁(х₁;у₁) и М₂(х₂;у₂), которые расположены в отношении

, - формулы координат середины отрезка М₁М₂, где М₁(х₁;у₁) и М₂(х₂; у₂).

_и - формулы для вычисления площади треугольника по трем точкам.

Задача 1. Дана точка М(3;2). Построить точки, симметричные с ней относительно оси абсцисс, оси ординат, начала координат. Определить координаты этих точек.

Анализ:

Чтобы найти симметричные точки, необходимо построить следующие графики функций: х=3, х=-3, у=2, у=-2.

Точка, симметричная т.М относительно оси абсцисс – это точка пересечения графиков х=3 и у=-2.

Точка, симметричная т.М относительно оси ординат – это точка пересечения графиков х=-3 и у=2.

Точка, симметричная т.М относительно начала координат – это точка пересечения графиков х=-3 и у=-2.

1. С помощью кнопки открыть окно двумерной графики. В диалоговое окно ввести первое уравнение х=3. Нажать вначале кнопку , затем . Аналогично построить остальные графики.

2. Чтобы найти координаты точки пересечения, необходимо подвести курсор к искомой точке и зафиксировать ее, нажав левую кнопку мыши. В левом нижнем углу экрана получим сообщение о координатах точки. Например, точка, симметричная относительно оси абсцисс имеет координаты: .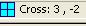

3. Построенные точки можно надписать с помощью кнопки .

Задача 2. Зная прямоугольные координаты точки А(3;4), найти ее полярные координаты.

1. Ввести в диалоговое окно формулу для вычисления полярного радиуса (x^2+y^2)^(1/2) и нажать .

2. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения x=3; y=4 и нажать кнопку . Получили полярную координату р точки А: р=5.

3. Ввести в диалоговое окно формулу для вычисления полярного угла tanα(у/х) и нажать .

4. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения x=3; y=4 и нажать кнопку .

5. В меню Solve выбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Задача 3. Найти прямоугольные координаты точки, если известны ее полярные координаты В(3; ), причем ось абсцисс совпадает с полярной осью, а начало координат с полюсом.

1. Ввести в диалоговое окно формулу для вычисления первой координаты 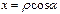и нажать .

2. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения р=3; α=-π/6 и нажать кнопку .

3. Чтобы найти приближенное значение полученного выражения в меню Simplifyвыбрать подменю . В появившемся диалоговом окне задать количество цифр после запятой и нажать кнопку . Получили ответ х=2,5.

4. Аналогично находим координату у по формуле 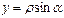. Получаем у=-1,5.

Задача 4. В полярной системе координат даны точки А(3; ) и В(2; ). Вычислить расстояние между ними.

1. Пусть координатам точки А (p;α) соответствуют А(3; ), a B(l;β) - В(2; ).

2. Ввести в диалоговое окно формулу для вычисления расстояния между двумя точками (p^2+l^2-2plcos(α-β))^(1/2) и нажать .

3. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения и нажать кнопку .

4. Чтобы найти приближенное значение полученного выражения в меню Simplifyвыбрать подменю . В появившемся диалоговом окне задать количество цифр после запятой и нажать кнопку .

Задача 5. Найдите расстояние между точками А (4; -2) и В (1; 2).

1. Ввести формулу для вычисления расстояния между двумя точками =((с-а)^2+(d-b)^2)^(1/2) в строку ввода диалогового окна Autor Expression и нажать , для вывода формулы в рабочее окно программы.

2. В меню Simplify выбрать подменю (или нажать кнопку ), ввести в появившемся окне значения а=4; в=-2; с=1; d=2 и нажать кнопку . Получили искомое расстояние: .

Задача 6. Дана точка М(-2;0), расстояние . Найти координату х, зная, что она лежит на биссектрисе первого и третьего координатных углов.

Использовать подстановку координат точки М(-2;0) в формулу для нахождения расстояние между двумя точками и уравнение биссектриса первого и третьего угла у=х. Решить полученное уравнение.

1. Ввести уравнение (х+2)^2+x^2)^(1/2)=10 в строку ввода и нажать кнопку .

2. Решить уравнение, используя меню Solve подменю .

Задача 7. Докажите, что четыре точки (4; 1), (0; 4), (-3; 0) и (1; -3) являются вершинами квадрата.

1. Найти расстояние , , и (см. задачу №5). Получим следующие значения: a=5, b=5, c=5, d=5. Получили правильный четырехугольник. Он будет являться квадратом, если хотя бы его диагонали перпендикулярны и один из углов прямой.

2. Найдем координаты вектора AB. Пусть координатам точки А (а; b) соответствуют А (1; 3), a B(c; d) - В (-2; 2).Для этого необходимо ввести в диалоговое окно формулу для вычисления координаты вектора х=с - а и нажать кнопку .

3. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения а=1; с=-2 и нажать кнопку . Получим первую координату вектора АВ х=-4.

4. Аналогично находят координату «у» вектора АВ по формуле y=d - b.

5. Аналогично находят координаты векторов BC, AC, BD.

6. Пусть координатам вектора АВ (а; b) соответствуют АВ (-4; 3), a BС(c; d) - ВС (-3; -4). Найти их скалярное произведение. Для этого ввести в диалоговое окно формулу для вычисления скалярного произведения .

7. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения а=-4; b=3; с=-3; d=-4 и нажать кнопку . Получим скалярное произведение p =0. Так как векторы не нулевые, следует что cos α=0 и α=90°.

8. Аналогично найти скалярное произведение векторов АС и BD. Оно тоже будет равно 0, следовательно векторы перпендикулярны. А значит ABCD – квадрат.

Задача 8. Найдите середину С отрезка АВ, если А (1; 3) и В (-3; 1).

1. Пусть координатам точки А (а;в) соответствуют А (1; 3), a B(c;d) - В (-3; 1).

2. Ввести в диалоговое окно формулу для вычисления координаты х=(а+с)/2 и нажать

3. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения а=1; с=-3 и нажать кнопку . Получили координату х точки С: х=-1

4. Аналогично находят координату «у» точки С по формуле y=(b+d)/2.

Задача 9. Найдите точку на оси абсцисс, равноудаленную от точек (-2; -3) и (7; 4).

Пусть (х;0) - искомая точка. Приравнивая расстояния от нее до данных точек, получим:

(х+2)²+(0+3)²=(х-7)²+(0-4)² или (х+2)²+9=(х-7)²+16.

1 способ: Ввести в диалоговое окно solve((x+2)^2+9=(x-7)^2+16,x) и нажать кнопку

. Получим х=2,88.

2 способ:

1. Ввести в диалоговое окно (х+2)^2+9=(х-7)^2+16 и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , 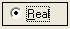и нажать кнопку . Получили х=2,88.

2. Чтобы найти приближенное значение полученного выражения в меню Simplifyвыбрать подменю . В появившемся диалоговом окне задать количество цифр после запятой и нажать кнопку .

Задача 10. Найдите периметр и площадь треугольника, если известны координаты его вершины А (1; 3), В (-2; 2) и С (-2; 0).

1. Найти расстояние , и (см. задачу №5). Получим следующие значения: , , .

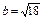2. Вести в диалоговое окно формулу для вычисления периметра треугольника и нажать кнопку .

3. В меню Simplifyвыбрать подменю (или нажать кнопку ) ввести в диалоговое окно значения а=2; b=10^(1/2); с=18^(1/2) и нажать кнопку . Получим периметр треугольника p = 3·√2 + √10 + 2.

4. Чтобы найти приближенное значение полученного выражения в меню Simplifyвыбрать подменю . В появившемся диалоговом окне задать количество цифр после запятой и нажать кнопку . Получили ответ р=9,5.

5. Далее аналогично находим площадь треугольника, используя формулы 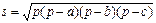и . Получили площадь s=3.

Задача 11. Найти вершины треугольника, зная середины его сторон: P(3;-2), Q(1;6), R(-4;2), а также вычислить площадь треугольника.

Если обозначить координаты: А(х₁;у₁), В(х₂;у₂), С(х₃;у₃). Тогда, чтобы найти вершины треугольника, надо решить две системы уравнений:

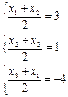
Площадь треугольника можно вычислить по следующей формуле:

S= (x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)).

1. Координаты точек: А(х₁;у₁) – А(a;b), В(х₂;у₂) – B(c;d), С(х₃;у₃) – C(e;f).

2. В меню Solve выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения:

Нажать кнопку . Получим a=-2, c=8, e=-6.

3. Аналогично решить систему (b+d)/2=-2

(d+f)/2=6

(b+f)/2=2.

4. Ввести в диалоговое окно формулу для вычисления площади треугольника и нажать .

5. В меню Simplify выбрать подменю (или нажать кнопку ), ввести в диалоговое окно значения а=-2; в=-6; с=8; d=2; e=-6; f=10 и нажать кнопку . Получили s=96.

Задачи для самостоятельного решения:

Дана точка М(-2;4). Построить точки, симметричные с ней относительно оси абсцисс, оси ординат, начала координат. Определить координаты этих точек.

[(-2,-4), (2,4), (2,-4)]

Построить точки, абсциссы которых равны –4, -2, -1, 0, 1, 2, 3 и 4, а ординаты определяются из уравнения у=3х-5 [О.Н. Цубербиллер, №28].

Найти координаты точек симметричных относительно биссектрисы второго координатного угла точкам 1) А(3; 5), 2) В(-4; 3), 3) С(7; -2).

[1) (-5.-3), 2) (-3,4), 3) (2,-7)]

Построить точки, координаты которых удовлетворяют уравнениям:

1) 2) [О.Н. Цубербиллер, №27, зад.1,2]

Зная прямоугольные координаты точек (-1;1), (0;2), (5;0), найти их полярные координаты.

Вычислить расстояние между двумя данными точками А(2; ) и В(1; ).

[ ]

На оси Х построить точку, равноудаленную от начала координат и от точки А(9;-3).

Найти расстояние от точки (-3;4) до

1) оси х; 2) оси у; 3) начала координат.

[1) 4; 2) 3; 3) 5]

Найти расстояние между точками:

1) (-6;3) и (0;-5) 2) (2;11) и (7;-1) [Судибор, №2.1]

[1) 10; 2) 13]

Найти точку пересечения медиан треугольника, зная координаты его вершин: (1;4), (-5;0), (-2;-1). [О.Н. Цубербиллер, Гл.II, п.3 №70]

[(-2.1)]

Дан треугольник А(4;1), В(7;5), С(-4;7). Найти точку пересечения биссектрисы угла А с противолежащей стороной ВС. [О.Н. Цубербиллер, №73]

[M(10/3;17/3)]

Найти центр тяжести четырехугольной однородной доски, зная, что углы доски помещаются в точках А(4;4), В(5;7), С(10;10), D(12;4). [О.Н. Цубербиллер, №84]

[x=8.2; y=6.2]

Зная две противоположные вершины ромба А(8;-3), С(10;11) и длину его стороны АВ=10, определить координаты остальных вершин ромба. [О.Н. Цубербиллер, №53]

[(-5,4)]

Доказать, что четырехугольник ABCD c вершинами в точках А(-1;-2), В(2;-5), С(1;-2), D(-2;1) является параллелограммом.

Доказать, что четырехугольник ABCD с вершинами в точках А(4;1), В(0,4), C(-3;0), D(1;-3) является квадратом.

Длина d отрезка MN равна 5; его проекция на ось абсцисс равна 4. Найти проекцию этого отрезка на ось ординат при условии, что он образует с осью ординат:

1) острый угол; 2) тупой угол. [Клетеник, №56]

[1) 3; 2) -3]

Дата добавления: 2015-10-23