
Читайте также:
|
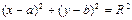 - уравнение окружности с центром в точке А (a; b) и радиусом R.
- уравнение окружности с центром в точке А (a; b) и радиусом R.
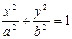 - каноническое уравнение эллипса, где
- каноническое уравнение эллипса, где 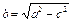 .
.
Эксцентриситетом эллипса называется число 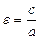
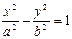 - уравнение гиперболы.
- уравнение гиперболы.
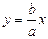 и
и  - уравнения асимптот гиперболы.
- уравнения асимптот гиперболы.
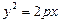 - уравнение параболы, где p – параметр.
- уравнение параболы, где p – параметр.
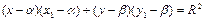 - уравнение касательной к окружности в точке
- уравнение касательной к окружности в точке 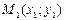
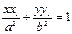 - уравнение касательной к эллипсу в точке
- уравнение касательной к эллипсу в точке 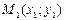
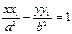 - уравнение касательной к гиперболе в точке
- уравнение касательной к гиперболе в точке 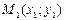
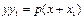 - уравнение касательной к параболе в точке
- уравнение касательной к параболе в точке 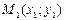
Задача 1. Найти на окружности заданной уравнением 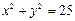 , точки а) с абсциссой 5; б) с ординатой 3.
, точки а) с абсциссой 5; б) с ординатой 3.
1. Ввести в диалоговое окно solve(5^2+y^2=25,y) и нажать кнопку  . Получим у=0. Искомая точка (5; 0).
. Получим у=0. Искомая точка (5; 0).
2.  Аналогично для точки у=3 ввести в диалоговое окно solve(x^2+3^2=25,x). Получим х=-4 и х=4. Искомые точки (-4;3) и (4;3).
Аналогично для точки у=3 ввести в диалоговое окно solve(x^2+3^2=25,x). Получим х=-4 и х=4. Искомые точки (-4;3) и (4;3).
Задача 2. Составить уравнение эллипса и построить, зная, что расстояние между фокусами равно 6 и большая полуось равна 5.
Так как а=5 с=3 находим b. Для этого вести в диалоговое окно формулу для вычисления b: b=(c^2-a^2)^(1/2).
В меню  выбрать подменю
выбрать подменю  (или нажать кнопку
(или нажать кнопку  ), ввести в диалоговое окно значения а=5; с=3 и нажать кнопку
), ввести в диалоговое окно значения а=5; с=3 и нажать кнопку  . Получили b=4.
. Получили b=4.
Ввести в диалоговое окно формулу уравнения эллипса: x^2/a^2+y^2/b^2=1.
В меню  выбрать подменю
выбрать подменю  (или нажать кнопку
(или нажать кнопку  ), ввести в диалоговое окно значения а=5; b=4 и нажать кнопку
), ввести в диалоговое окно значения а=5; b=4 и нажать кнопку  . Получили уравнение эллипса.
. Получили уравнение эллипса.

С помощью кнопки  открыть окно двумерной графики и нажать кнопку
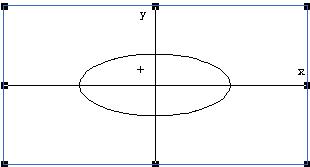
открыть окно двумерной графики и нажать кнопку  . Получим график эллипса.
. Получим график эллипса.
Задача 3. Вычислить площадь треугольника, образованного асимптотами гиперболы 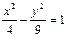 и прямой
и прямой 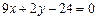 .
.
1) Вычислим a и b. Для этого вводим в диалоговое окно a=4^(1/2).
2) В меню Simplifyвыбрать подменю  . Получим а=2.
. Получим а=2.
3) Аналогично вычисляет b.
4) Вводим в диалоговое окно уравнение асимптоты y=(b/a)x.
5) В меню Simplifyвыбрать подменю  (или нажать кнопку
(или нажать кнопку  ) ввести в диалоговое окно значения а=2; b=3 и нажать кнопку
) ввести в диалоговое окно значения а=2; b=3 и нажать кнопку  . Получим уравнение одной из асимптоту у=3х/2.
. Получим уравнение одной из асимптоту у=3х/2.
6) Аналогично находим уравнение второй асимптоты (формула - y=-(b/a)x).
7) Решаем 3 системы уравнений: у=3х/2. и у=-3х/2; у=3х/2 и 9х+2у-24=0; у=-3х/2 и 9х+2у-24=0. получаем три точки – вершины треугольника – (0;0), (2;3), (4;-6).
8) Вводим в диалоговое окно формулу для вычисления площади треугольника по трем точкам s=((c-a)(f-b)-(e-a)(d-b))/2.
9) В меню Simplifyвыбрать подменю  (или нажать кнопку
(или нажать кнопку  ) ввести в диалоговое окно значения а=0; b=0, c=2, d=3, e=4, f=-6 и нажать кнопку
) ввести в диалоговое окно значения а=0; b=0, c=2, d=3, e=4, f=-6 и нажать кнопку  . Получим s=12.
. Получим s=12.
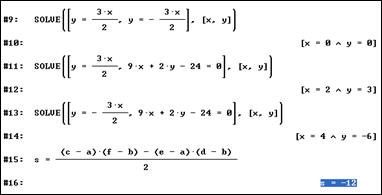
Задача 4. Найти точки пересечения параболы 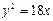 с прямой
с прямой 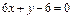 (О.Н. Цубербиллер, Гл. V, п. 4, № 488 (п.1)).
(О.Н. Цубербиллер, Гл. V, п. 4, № 488 (п.1)).
В меню  выбрать подменю
выбрать подменю  . В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения: y^2=18x, 6x+y-6=0.
. В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения: y^2=18x, 6x+y-6=0.
Нажать кнопку  . Получим х=2, у=-6 и x=1/2, y=3.
. Получим х=2, у=-6 и x=1/2, y=3.
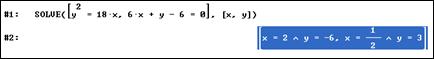
Дата добавления: 2015-10-23; просмотров: 226 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Глава 3. Линии первого порядка. | | | Двойное векторное произведение векторов. |