
Читайте также:
|
 - формула проекции вектора
- формула проекции вектора  на ось и.
на ось и.
 - формула для вычисления модуля вектора.
- формула для вычисления модуля вектора.
 - формула для вычисления суммы векторов.
- формула для вычисления суммы векторов.
 - формула для вычисления разности векторов.
- формула для вычисления разности векторов.
 - формула для вычисления умножения вектора на число.
- формула для вычисления умножения вектора на число.
 - формула для вычисления скалярного произведения векторов.
- формула для вычисления скалярного произведения векторов.
 - формула для вычисления векторного произведения векторов.
- формула для вычисления векторного произведения векторов.
 - формула для вычисления смешанного произведения векторов.
- формула для вычисления смешанного произведения векторов.
 - формула для вычисления двойного векторного произведения векторов
- формула для вычисления двойного векторного произведения векторов
Задача 1. Даны векторы  ,
,  и
и  . Найдите координаторы вектора: 1)
. Найдите координаторы вектора: 1)  , 2)
, 2) 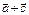 , 3)
, 3)  . [Баврин, Гл.2, №8]
. [Баврин, Гл.2, №8]
Определим данные вектора: а:=[2,3,0], b:=[-1,2,3], c:=[3,1,0].
Найдем вектор  . Для этого ввести в диалоговое окно выражение а+b и нажать кнопку
. Для этого ввести в диалоговое окно выражение а+b и нажать кнопку  . Затем в меню Solveвыбрать подменю
. Затем в меню Solveвыбрать подменю  . В диалоговом окне поставить флажки
. В диалоговом окне поставить флажки  ,
,  и нажать кнопку
и нажать кнопку  .
.
Аналогично, найти 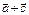 и
и  .
.

Задача 2. Найдите скалярное произведение векторов  ,
, 
Определим данные вектора: а:=[4,-2,1], b:=[1,2,3].
Найдем скалярное произведение векторов.. Для этого ввести в диалоговое окно выражение а*b и нажать кнопку  . Затем в меню Solveвыбрать подменю
. Затем в меню Solveвыбрать подменю  . В диалоговом окне поставить флажки
. В диалоговом окне поставить флажки  ,
,  и нажать кнопку
и нажать кнопку  .
.
Получим, ab=3.

Задача 3. Найти векторное произведение векторов a={2,3,1} b={5,6,4} [Игудесман, Ч.2, 1, №4]
Определим данные вектора: а:=[2,3,1], b:=[5,6,4].
Найдем скалярное произведение векторов.. Для этого ввести в диалоговое окно выражение cross(а,b) и нажать кнопку  . Затем в меню Solveвыбрать подменю
. Затем в меню Solveвыбрать подменю  . В диалоговом окне поставить флажки
. В диалоговом окне поставить флажки  ,
,  и нажать кнопку
и нажать кнопку  .
.

Задача 4. Компланарны ли векторы a,b,c: a={7,3,4}, b={-1,2,-1}, c={4,2,4}. [Кузнецов, АГ, №5]
1 способ:
Определим данные вектора: а:=[7,3,4], b:=[-1,2,-1], c:=[4,2,4].
Найдем смешанное произведение векторов. Для этого ввести в диалоговое окно выражение а*cross(b,с) и нажать кнопку  . Затем в меню Solveвыбрать подменю
. Затем в меню Solveвыбрать подменю  . В диалоговом окне поставить флажки
. В диалоговом окне поставить флажки  ,
,  и нажать кнопку
и нажать кнопку  .
.
Получим смешанное произведение не равно 0, следовательно вектора не компланарны.

2 способ:
Ввести матрицу М. для этого вести в диалоговое окно M:= [7, 3, 4; -1, 2, -1; 4, 2, 4] и нажать кнопку  .
.
Вычислить определитель матрицы. Для этого ввести в диалоговое окно выражение det(M) и нажать кнопку  . Затем в меню Solveвыбрать подменю
. Затем в меню Solveвыбрать подменю  . В диалоговом окне поставить флажки
. В диалоговом окне поставить флажки  ,
,  и нажать кнопку
и нажать кнопку  .
.
Получим смешанное произведение не равно 0, следовательно вектора не компланарны.

Задача 5. Вычислить объем тетраэдра с вершинами в точках A, B, C, D и его высоту, опущенную из вершины D на грань ABC. A(0,-1,-1), B(-2,3,5), C(1,-5,-9), D(-1,-6,3). [Кузнецов, АГ, №6]
Найдем координаты векторов  ,
, 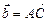 ,
,  . Для этого введем в диалоговое окно a:= [g - d, h - e, k - f] и нажать
. Для этого введем в диалоговое окно a:= [g - d, h - e, k - f] и нажать  . В меню
. В меню  выбрать подменю
выбрать подменю  (или нажать кнопку
(или нажать кнопку  ), ввести в появившемся окне соответствующие значения координат точек и нажать кнопку
), ввести в появившемся окне соответствующие значения координат точек и нажать кнопку  .
.
Аналогично, найти координаты остальных векторов.

По формуле нахождения объема тетраэдра  , находим объем данного тетраэдра.
, находим объем данного тетраэдра.

Из другой формулы нахождения объема тетраэдра  , находим искомую высоту, предварительно вычислив площадь грани АВС -
, находим искомую высоту, предварительно вычислив площадь грани АВС -  .
.

Получим V=37/3, h=37/33.
Дата добавления: 2015-10-23; просмотров: 278 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Полярное уравнение эллипса, гиперболы и параболы. | | | Декартовы прямоугольные координаты в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении. |