Глава 3. Линии первого порядка.

Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности перпендикулярности двух прямых.

Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой «в отрезках».

Задача определения расстояния от точки до прямой.

Уравнение пучка прямых.

Полярное уравнение прямой.

и 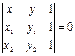- формулы уравнения прямой, проходящей через две данные точки М₁(х₁;у₁) и М₂(х₂;у₂).

- формула уравнения прямой с угловым коэффициентом, где , , α – угол, образованный прямой с положительным направлением оси абсцисс, b – величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

- общее уравнение прямой

Расположение прямой относительно осей координат, если ее уравнение :

1. . Уравнение прямой принимает вид . Прямая параллельна оси х. Если и , прямая совпадает с осью х.
2. . Уравнение прямой принимает вид . Прямая параллельна оси у и совпадает, если .
3. . Прямая проходит через начало координат.

Задача 1. Найдите точку пересечения прямых, заданных уравнениями и .

1 способ:

1. В меню Solve выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК.

2. В новом диалоговом окне ввести уравнения:

3. Нажать кнопку . Получим х=-1, у=2.

2 способ (графический)

1. С помощью кнопки открыть окно двумерной графики. Ввести первое уравнение х-у+3=0. Нажать кнопку , затем повторно . Аналогично построить второй график функции 4х-у+6=0.

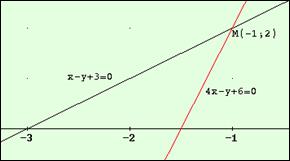
Чтобы найти координаты точки пересечения, необходимо подвести курсор к искомой точке и зафиксировать ее, нажав левую кнопку мыши. В левом нижнем углу экрана получим сообщение о координатах точки:

2. Полученный график можно надписать с помощью кнопки .

Задача 2. Даны прямые: у=2х+3 и у=-х+4.

а) Проверить, проходят ли они через точки А(-1;1), В(4;0), С(3;1), D(0;0).

в) Найти точку пересечения прямых.

1. Ввести в диалоговое окно уравнение прямой у=2*х+3 и нажать .

2. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно координаты точки А: x=-1; y=1 и нажать кнопку . Получили равенство 1=1 (т.е. точка А принадлежит прямой у=2х+3). Аналогично проверяем остальные точки (точки В, С, D y=2x+3)

3. Аналогично проверяем, какие из точек принадлежат прямой у=-х+4 (точки В и С у=-х+4; точки А и D у=-х+4).

4. Чтобы найти точку пересечения прямых, необходимо в меню выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения: у=2*х+3, у=-х+4. Нажать кнопку . Получим х=1/3, у=11/3.

5. Чтобы найти приближенное значение полученных корней, в меню выбрать подменю . В появившемся диалоговом окне задать количество цифр после запятой и нажать кнопку .

Задача 3. Написать уравнение прямой, которая проходит через точку А(3;-1) и параллельна: 1) оси абсцисс; 2) биссектрисе 1-го и 3-го координатного угла; 3) прямой у=3х+7.

Уравнение прямой имеет вид: у=kx+b.

Параметр k характеризует направление прямой и называется ее угловым коэффициентом: , - угол, образованный прямой с положительным направлением оси абсцисс.

1. Рассмотрим 1) случай: ввести в диалоговое окно уравнение прямой у=tan() и нажать .

2. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно угол =0^о (т.к. уравнение прямой, проходящее через точку А(3;-1), параллельно оси х =0^о) и нажать кнопку .

3. Чтобы найти из уравнения у=kx+b, параметр b, необходимо ввести в диалоговое окно у=k*x+b, нажать . Затем в меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно координаты точки А: х=3, у=-1, k=0 и нажать кнопку . Получили b=-1.

4. Теперь найдем искомое уравнение: выделить уравнение у=k*x+b, в меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно k=0, b=-1 и нажать кнопку . Получили y=-1.

5. Рассмотрим 2) случай: ввести в диалоговое окно уравнение прямой у=tan() и нажать .

6. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно угол = 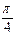(т.к. биссектриса координатного угла образует с осью х угол = 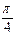) и нажать кнопку . Затем аналогично 1) случаю найти параметр b и уравнение прямой.

7. Рассмотрим 3) случай. Необходимо составить уравнение прямой, проходящей через точку А(3;-1), параллельное прямой у=3х+7 коэффициент k нового уравнения равен 3. Далее аналогично 1) случаю найти параметр b и уравнение прямой.

Задача 4. Даны вершины треугольника: А(4;6), В(-4;0), С(-1;-4). Составить уравнения: 1) трех его сторон; 2) медианы, проведенной из вершины С; 3) биссектрисы угла В; 4) высоты, опущенной из вершины А на сторону ВС.

1) Уравнения трех сторон.

1. Обозначим А(4;6) – А(а;b), В(-4;0) – В(c;d).

2. Ввести в диалоговое окно формулу для нахождения уравнения прямой:

(y-b)/(d-b)=(x-a)/(c-a) и нажать .

3. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно значения а=4, b=6, c=-4, d=0 и нажать кнопку . Получим уравнение стороны АВ: у=3(х+4)/4.

4. Аналогично найти уравнения сторон ВС и АС.

2) Уравнение медианы, проведенной из вершины С.

1. Найти координаты середины отрезка АВ. Для этого необходимо ввести в диалоговое окно формулы середины отрезка: х=(а+с)/2, у=(b+d)/2 и нажать .

2. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно значения а=4, b=6, c=-4, d=0 и нажать кнопку . Получим х=0, у=3.

3. По двум точкам С(-1;-4) и М(0;3) найти уравнение медианы (см. случай 1.)

3) Уравнение биссектрисы угла В.

=ВА=

=ВС=

.

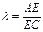Координаты точки Е: , .

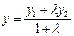1. Ввести в диалоговое окно формулу для вычисления расстояния между двумя точками =((с-а)^2+(d-b)^2)^(1/2) и нажать .

2. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно значения а=4; в=6; с=-4; d=0 и нажать кнопку . Получили =ВА=10. Аналогично найдем =ВС=5. .

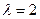3. Ввести в диалоговое окно формулы для вычисления координаты Е, затем подставить значения. Получим Е(2/3;-2/3).

4. По двум точкам В(-4;0) и Е(2/3;-2/3) найти уравнение биссектрисы (см. случай 1.)

4) Уравнение высоты, опущенной из вершины А на сторону ВС.

1. Ввести в диалоговое окно k=3/4 (т.к. , 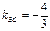из уравнения стороны ВС: у=(-4х+16)/3) и нажать .

2. Также ввести уравнение прямой у=k*х+b и подставить в него k=3/4 и координаты точки А: х=4, у=6. Получим b=3.

3. Подставить в уравнение прямой у=kx+b: k=3/4 и b=3. Получим уравнение высоты.

Задача 5. Какой угол образует с осью Х прямая, проходящая через точки М(0;2) и N(-2;4)?

1. Введем обозначения М(0;2) – М(a;b), N(-2;4) – N(c;d).

2. Ввести в диалоговое окно формулу для вычисления угла tan(x)=(d-b)/(c-a) и нажать .

3. В меню выбрать подменю (или нажать кнопку ), ввести в диалоговое окно значения а=0; в=2; с=-2; d=4 и нажать кнопку . Получили искомое расстояние: .

4. В меню 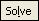выбрать подменю . В диалоговом окне поставить флажки 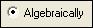, и нажать кнопку .

Задача 6. Докажите, что прямые , не пересекаются.

1. В меню Solve выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК.

2. В новом диалоговом окне ввести уравнения , .

3. Нажать кнопку . Получили, что система не имеет решений, следовательно, прямые не пересекаются.

Задачи для самостоятельного решения:

Найти точки пересечения с осями координат прямой, заданной уравнением:

1) х+2у+3=0; 2) 4х-2у-10=0.

[(7/5;-11/5]

Составьте уравнение прямой, которая проходит через точки А(-1;1), В(1;0).

[ 2y+x-1=0 ]

Докажите, что прямые х+2у=3, 2х-у=1 и 3х+у=4 пересекаются в одной точке.

[(1,1)]

Докажите, что прямые х+2у=3 и 2х+4у=3 не пересекаются.

Написать уравнение прямой, соединяющей центр тяжести треугольника АВС с началом координат, причем координаты вершин такие: А(2,-1), В(4,5), С(-3,2). [Цубербиллер, №215]

[ у=2х ]

Проверить, что четыре точки А(-2,-2), В(4,5), С(7,7) и D (3,1) служат вершинами трапеции, и составить уравнения средней линии и диагоналей трапеции. [Цубербиллер, №217]

[ ; ; ; ]

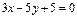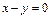Вычислить угол между прямыми: 1) 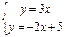; 2) ; 3) . [Цубербиллер, №196]

[ ]

Найти отрезки, отсекаемые на осях координат следующими прямыми: , , и . [Цубербиллер, №227]

[a=-4, b=6; a-1/2, b=-2; a=1, b=1; a=-4, b=-10]

Найти расстояние прямой от начала координат. [Цубербиллер, №239]

[2/3]

Найти расстояние точки:

a. А(2,7) от прямой ;

b. В(-3,5) от прямой ;

c. С(-3,2) от прямой ;

d. D(8.5) от прямой .[Цубербиллер, №245, п.2,3,4,5]

.[1) 4, 2) 17/3; 3) 0; 4) -2,2]

Через начало координат провести прямую параллельно прямой . [Цубербиллер, №279]

[ ]

Даны уравнения сторон треугольника: , и . Вычислить координаты его вершин.

[(3,0), (0,-5), (-2,1)]

Установить, какие из следующих пар прямых перпендикулярны (Д.В. Клетеник №264):

1) 3х-у+5=0 2) 3х-4у+1=0 3) 6х-15у+7=0

х+3у-1=0 4х-3у+7=0 10х+4у-3=0

4) 9х-12у+5=0 5) 7х-2у+1=0 6) 5х-7у+3=0

8х+6у-13=0 4х+6у+17=0 3х+2у-5=0

[Перпендикулярны 1), 3) и 4).]

Проверить, проходят ли через одну и ту же точку следующие три прямые:

1) ; 2) ; 3) .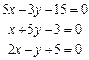

[1 и 2 проходят через одну точку, 3 – не проходит]

13. Установить, какие из следующих пар прямых перпендикулярны (Д.В. Клетеник №264):

1) 3х-у+5=0 2) 3х-4у+1=0 3) 6х-15у+7=0

х+3у-1=0 4х-3у+7=0 10х+4у-3=0

4) 9х-12у+5=0 5) 7х-2у+1=0 6) 5х-7у+3=0

8х+6у-13=0 4х+6у+17=0 3х+2у-5=0

[Перпендикулярны 1), 3) и 4)]

Дата добавления: 2015-10-23