Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой.

- уравнение определяет плоскость, проходящую через точку и имеющую нормальный вектор .

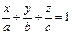- уравнение плоскости в отрезках, где

- уравнение плоскости, определенное тремя точками.

Прямая как пересечение двух плоскостей определяется совместным зада­нием двух уравнений первой степени:

- каноническое уравнение прямой.

- уравнение прямой, заданной двумя точками.

- параметрическое уравнение прямой.

Задача 1. Проходит ли плоскость через одну из следующих точек: А(-1,6,3), В(3,-2,-5), С(0,4,1), D(2,0,5), E(2,7,0), F(0,1,0)? [Цубербиллер, Гл.9, №753]

Ввести формулу уравнения плоскости в строку ввода диалогового окна Autor Expression и нажать , для вывода формулы в рабочее окно программы.

В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения координат точки и нажать кнопку . Получим верное равенство, следовательно данная плоскость проходит через точку А(-1,6-3).

Аналогично проверяем остальные точки. Получим, данная плоскость проходит через точки А, В, С, F.

Задача 2. Вычислить расстояние точки (3,1,1) от плоскости 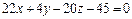. [Цубербиллер, Гл.9, 771, п.1]

Ввести коэффициенты уравнения плоскости и координаты данной точки.

Ввести в диалоговое окно формулу для вычисления расстояния точки от плоскости ABS((a·x + b·y + c·z + d)/(a^2 + b^2 + c^2)^(1/2)) и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения и нажать кнопку .

Получим, расстояние равно 3/2.

Задача 3. Вычислить высоту 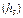пирамиды с вершинами S(0,6,4), А(3,5,3), В(-2,11,-5) и С(1,-1,4). [Цубербиллер, Гл.9, 772]

Ввести матрицу М. для этого вести в диалоговое окно M:= [x, y, z, 1; 3, 5, 3, 1; -2, 11, -5, 1; 1, -1, 4, 1] и нажать кнопку .

Вычислить определитель матрицы. Для этого ввести в диалоговое окно выражение det(M) и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Получим уравнение плоскости .

Ввести коэффициенты уравнения плоскости и координаты точки S.

Ввести в диалоговое окно формулу для вычисления расстояния точки от плоскости ABS((a·x + b·y + c·z + d)/(a^2 + b^2 + c^2)^(1/2)) и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения и нажать кнопку .

Получим, высота пирамиды равна 3.

Задача 4. Проверить, можно ли провести плоскость через следующие четыре точки: (3,1,0), (0,7,2), (-1,0-5) и (4,1,5). [Цубербиллер, Гл.9, 789]

Ввести матрицу М. для этого вести в диалоговое окно M:= [3, 1, 0, 1; 0, 7, 2, 1; -1, 0, -5, 1; 4, 1, 5, 1] и нажать кнопку .

Вычислить определитель матрицы в символьном виде. Для этого ввести в диалоговое окно выражение det(M) и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Получим, определитель не равен нулю, следовательно через данные четыре точки нельзя провести плоскость.

Задача 5. Проверить, имеют ли общую точку следующие четыре плоскости: , , , .

В меню Solve выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения данные уравнения.

Нажать кнопку .

Получим одно решение, следовательно, все четыре плоскости имеют одну общую точку.

Задача 6. Найти каноническое уравнение прямой . [Шипачев В.С., стр.249, пример 1.]

Полагая, например, 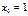, решим полученную систему. В меню Solve выбрать подменю . В появившемся окне задать количество уравнений и нажать ОК. В новом диалоговом окне ввести уравнения данные уравнения. Нажать кнопку .

Получим, координаты точки М(1,2,1) данной прямой.

Определим направляющие вектора: и . Ввести данные вектора:

Найдем векторное произведение векторов. Для этого ввести в диалоговое окно выражение cross(a,b) и нажать кнопку . Затем в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Затем подставляем полученные значения в формулу канонического уравнения прямой.

Получим искомое уравнения данной прямой.

Задача 7. Покажите, что прямая перпендикулярна к прямой 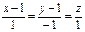. [Баврин И.И., Гл.3, №18]

Анализ: Условие перпендикулярности прямых есть условие перпендикулярности их направляющих векторов.

Ввести направляющие вектора.

Найти скалярное произведение данных векторов.

Получим, скалярное произведение равно нулю, следовательно, векторы перпендикулярны, а это значит, что данные прямые тоже перпендикулярны.

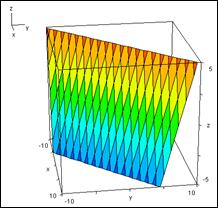
Задача 8. Постройте плоскости , , . [Баврин И.И., Гл.3, №6]

С помощью кнопки открыть окно трехмерной графики. В диалоговое окно ввести уравнение . Нажать вначале кнопку , затем .

Аналогично построить остальные графики.

Задача 9. Найти точку пересечения прямой и плоскости. [Цубербиллер Гл.10, №828]

Анализ: Обозначим три равных отношения, входящих в уравнение данной прямой, через р. Вставляя эти значения в уравнение плоскости, найдем значение этого параметра, затем, следовательно, и координаты искомой точки

Ввести координаты искомой точки. Для этого ввести в диалоговое окно выражение x:=4p+12 и нажать кнопку . Аналогично ввести выражения y:=3p+9 и z:=p+1.

Ввести в диалоговое окно выражение a·x + b·y + c·z + d = 0 и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения коэффициентов уравнения плоскости и нажать кнопку .

Затем полученное выражение упростить относительно р. Для этого в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Затем подставив значение р в первые три уравнения найдем координаты точки пересечения.

Дата добавления: 2015-10-23