Поверхности второго порядка.

- уравнение сферы с центром в точке С(a,b γ) и радиусом r.

- уравнение касательной плоскости к сфере.

- уравнение эллипсоида.

- уравнение однополостного гиперболоида.

- уравнение двуполостного гиперболоида.

- уравнение эллиптического параболоида.

- уравнение гиперболического уравнения.

Задача 1. Составить уравнение сферы в каждом из следующих случаев:

1) сфера имеет центр С (5; — 3; 7) и радиус r= 2;

2) сфера проходит через точку А (2; — 1; — 3) и имеет центр С (3; —2; 1).

[Клетеник, №1084, п.2,4]

п.1:

Ввести в диалоговое окно уравнение, определяющее сферу (x - a)^2 + (y - b)^2 + (z - c)^2 = r^2 и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения координат центра сферы и нажать кнопку .

Получим, искомое уравнение.

п.2:

Для нахождения радиуса сферы, необходимо найти расстояние между двумя данными точками: для этого ввести в диалоговое окно формулу для вычисления расстояния между двумя точками ((d - a)^2 + (e - b)^2 + (f - c)^2)^(1/2) и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения координат данных точек и нажать кнопку .

Для нахождения уравнения искомой сферы, необходимо выделить в активном окне первую формулу (т.е. уравнение определяющее сферу) и в меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения координат центра сферы и нажать кнопку .

Задача 2. Определить центр и радиус сферы .

Анализ: Точка О(3,-2,1), нормальный вектор плоскости . Уравнение прямой, проходящей через точку О и перпендикулярной плоскости имеет вид , а следовательно .

Ввести координаты точки прямой. Для этого ввести в диалоговое окно выражение x:=3+2t и нажать кнопку . Аналогично ввести выражения y:=-2-2t и z:=1-t.

Ввести в диалоговое окно выражение a·x + b·y + c·z + d = 0 и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения коэффициентов уравнения плоскости и нажать кнопку .

Затем полученное выражение упростить относительно р. Для этого в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Затем подставив значение р в первые три уравнения найдем координаты центра.

Найдем расстояние от точки О до плоскости. Для этого ввести в диалоговое окно формулу для нахождения расстояния от точки до плоскости ABS((a·e + b·f + c·g + d)/(a^2 + b^2 + c^2)^(1/2)) и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения коэффициентов уравнения плоскости и координаты точки О и нажать кнопку .

Получим р=6.

Найдем искомый радиус. Для этого ввести в диалоговое окно формулу для нахождения радиуса (r^2 - p^2)^(1/2) и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения и нажать кнопку .

Получим, центр сферы С(-1,2,3) и r=8.

Задача 3. Построить поверхность . [Минорский, №573, п.1]

С помощью кнопки открыть окно трехмерной графики. В диалоговое окно ввести уравнение (x^2+y^2/2)/2. Нажать вначале кнопку , затем .

Задача 4. Найти точки пересечения поверхности: 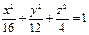с прямой [Цубербиллер, №904, п.1]

Анализ: Обозначим три равных отношения, входящих в уравнение данной прямой, через р. Вставляя эти значения в уравнение поверхности, найдем значение этого параметра, затем, следовательно, и координаты искомой точки

Ввести координаты искомой точки. Для этого ввести в диалоговое окно выражение x:=2p+4 и нажать кнопку . Аналогично ввести выражения y:=-3p-6 и z:=-2p-2.

Ввести в диалоговое окно уравнение поверхности x^2/a + y^2/b + z^2/c = 1 и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения коэффициентов уравнения плоскости и нажать кнопку .

Затем полученное выражение упростить относительно р. Для этого в меню Solveвыбрать подменю . В диалоговом окне поставить флажки , и нажать кнопку .

Затем подставив значение р в первые три уравнения найдем координаты одной точки пересечения: А(0,0,2).

Аналогично подставив второе значение р, найдем координаты второй точки пересечения: В(2,-3,0).

Задача 5. Найти плоскость, касающуюся конуса 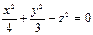в точке (4,-6,4)

Ввести в диалоговое окно уравнение конуса xd/a+ye/b-zf/c=0 и нажать кнопку . В меню выбрать подменю (или нажать кнопку ), ввести в появившемся окне соответствующие значения коэффициентов уравнения и координаты данной точки, и нажать кнопку .

Дата добавления: 2015-10-23