Дифференциальное уравнение термализации нейтронов

При термализации нейтронов их кинетические энергии сравнимы с кинетическими энергиями ядер. Поэтому энергия нейтрона, сталкивающегося с ядром, может как уменьшаться, так и увеличиваться. В этом и состоит основная трудность расчета спектра тепловых нейтронов, даже если не учитывать химические связи. Здесь мы не будем выводить уравнение термализции, а приведем лишь некоторые физические соображения, которые помогут записать это уравнение.

0,001

0,01

0,1

Е, эВ

Ф_т

Рис. 19.4

Рассмотрим для простоты бесконечную среду со слабым поглощением, В такой средетепловые нейтроны распределены по спектру, близкому к максвелловскому (5.1), а замедляющиеся - по спектру Ферми:

Ф(Е)=[S₀/(xå_sE)] *Exp{- 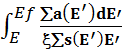} (5.3)

Предположим, что в качестве замедлителя выбран одноатомный тяжелый газ (A>>1). В случае тяжелого газа передача энергии от ядер замедлителя и обратно происходит малыми порциями. Уравнение, характеризующее такой процесс передачи энергии, есть дифференциальное уравнение второго порядка (уравнение диффузии). Запишем его для средыбез источников и при отсутствии поглощения:

kТФ’’_м(E) + Ф’_м(Е)+ Ф_м(Е)/Е = 0 (5.4)

Здесь штрихи обозначают первую и вторую производную по энергии

Легко проверить, что решением этого уравнения является спектр Максвелла, в котором средние энергии нейтронов и ядер замедлителя одинаковы.

При больших энергиях нейтронов (E>>kT) дифференциальное уравнение для спектра Ферми можно написать в виде:

Ф’_ф(E) + Ф_ф(E)/E + å_a (E)/(xå_sE) *Ф_ф (E)= 0 (5.5)

Естественно предположить, что должно существовать уравнение, объединяющее эти два:

kTФ’’(E) + Ф’(E)+ {1+ å_a (E)/(xå_s}*( Ф(E)/E) =0 (5.6)

При kT=0 оно переходит в уравнение для замедляющихся нейтронов (5.5), а при å_a =0 - для тепловых (5.5). Перепишем уравнение (5.6), вводя безразмерную энергию z = E/kT и предполагая, как обычно, что сечения поглощения в тепловой области меняются по закону 1/v:

Ф’’(z)+ Ф’(z) +{1-α/ √z} Ф(z)/z=0 (5.7)

Где параметр α= å_a (kT)/(xå_s)

В среде со слабым поглощением истинный спектр нейтронов незначительно отличается от спектра Максвелла и поэтому поток можно представить следующим образом:

Ф(z)=Ф_м (z) *β(z)

где β(z) -поправка к спектру Максвелла. Вычисляя первую и вторую производные Ф(z) и подставляя полученные значения в уравнение (5.7), получаем дифференциальное уравнение для поправки β(z). Таким образом можно вычислить эти поправки и решить задачу.

В заключение рассмотрим способ вычисления энергии сшивки Е^с_гр. Из условия равенства потоков:

Ф_м(Е^с_гр)=Ф_ф (Е^с_гр)

Получается трансцендентное уравнение для z:

Z²_грexp(-Z_гр) =(√π/2) α

Таким образом, хотя и с громоздкими вычислениями задача термализации все же решается.

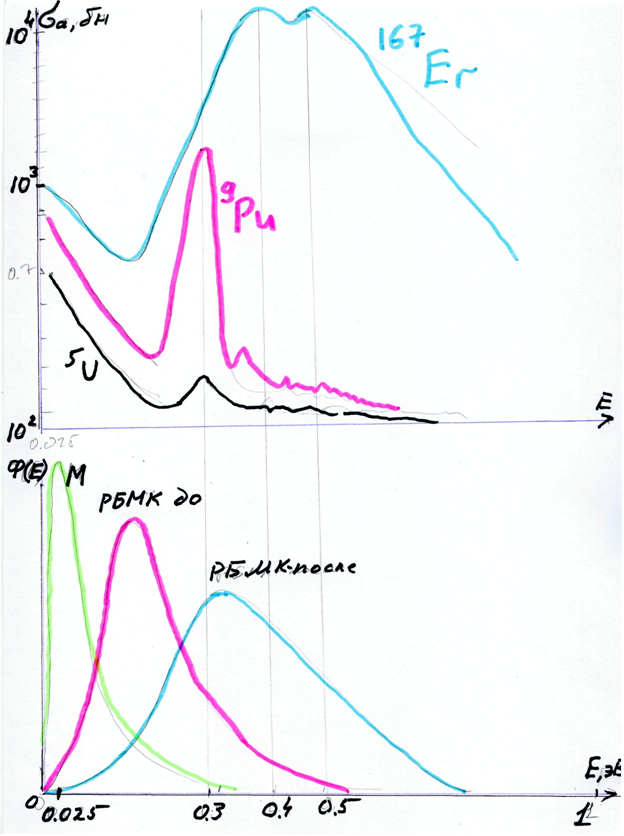
Насколько важны соображения по выбору спектра и спектральная компонента обратных связей в уран-графитовых реакторах видно на примере их конструкций.

Диффузионный разогрев и охлаждение спектра можно оценить по формуле.

Т_нг =Т₁[1+1.4*å_а(kT₁)/xå_s(1эВ)]

Изменение основных характеристик гражданских уран -графитовых реакторов в процессе их эволюции представлено в таблице 0.

Изменение характеристик Уран-графитовых реакторов.

Реактор	Обогащение %	Конструк ционный	Шаг реш,мм	|Безопасность Паровой/Мощн
I –АЭС, Билибино		н/ст		<0
АМБ, Белоярск		н/ст		<0
РБМК-до 86		Zr		>>0 (6β)
РБМК-после 86	2.4-2.8+Er	Zr		>=0
РБМК 5й КАЭС	2.4-2.8+Er	Zr	220?	<0

При проектировании РБМК упор делался на экономичность (а проще- на дешевизну) строительства и эксплуатации блока. Поэтому, исходя из этой концепции, были приняты меры по снижению по возможности всех затрат:

Основные нейтронно-физические свойства реактора следуют из особенностей принятой концепции (см. табл 1-3).

1. ТОПЛИВО. Поскольку применяется Графит и в реакторе формируется мягкий спектр нейтронов то.

a. Это дает возможность использовать малообогащенное топливо с обогащением до/около 2%. К сожалению, при этом баланс поглощения по мере выгорания топлива становится очень плохим (неустойчивым по отношению к выпариванию воды из канала): соответственно, и паровой и мощностной коэффициенты реактивности (a_j и a_W) – становятся просто опасными.

b. Для исправления неудачного баланса и обеспечения ядерной Безопасности приходится переходить на обогащение топлива не менее 2.4% (тогда баланс хоть как-то приемлем).

Дата добавления: 2015-10-26