Вычисление площади плоской фигуры.

Согласно свойству 4 двойного интеграла площадь области плоскости Oxy выражается формулой .

Пример 5. Найдём площадь фигуры , ограниченной линиями , , . Опишем область системой неравенств, для чего определим точки пересечения линий: . Из рисунка следует, что 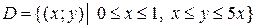. Имеем тогда: (кв.ед.).

3. Вычисление площади поверхности.

Пусть в пространстве задана гладкая поверхность , определяемая уравнением . Если поверхность однозначно проектируется на область плоскости Oxy, то площадь поверхности находится по формуле

. (15)

Пример 6. Вычислим площадь части поверхности параболоида вращения , ограниченной цилиндром . Проекцией поверхности на плоскость является область . Имеем , 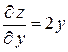. По формуле (15) площадь поверхности равна . Переходя к полярным координатам, получаем: = (кв.ед.).

4. Вычисление массы тонкой пластинки.

Пусть на плоской области распределено некоторое вещество. Выделим в произвольную часть площадью . Пусть масса вещества, приходящаяся на , составляет . Отношение называется средней поверхностной плотностью вещества в области . Будем теперь уменьшать область , стягивая её в точку ; площадь при этом будет стремиться к нулю. Если существует предел , то он называется поверхностной плотностью вещества в точке М и является функцией этой точки:

. (16)

Тонкую пластинку мы можем рассматривать как массу, непрерывно распределённую с поверхностной плотностью по плоской области . Разобьём область на части с площадями соответственно, столь малые, что плотность в каждой части 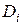будем считать постоянной и равной плотности в произвольно выбранной точке .

Тогда сумма приближённо выражает массу всей пластинки, причём тем точнее, чем меньше размеры частичных областей . Точное значение массы равно пределу этой суммы при и стремлении к нулю наибольшего из диаметров частичных областей . С другой стороны, этот предел равен двойному интегралу от функции по области . Получаем формулу вычисления массы тонкой пластинки: , или

, (17)

если область является частью плоскости .

5. Вычисление координат центра тяжести плоской фигуры.

Пусть плоская фигура занимает область в плоскости . Если по ней непрерывно распределена масса с поверхностной плотностью , то координаты центра тяжести плоской фигуры определяются по формулам

, , (18)

где – масса фигуры, вычисляемая по формуле (17), а выражения

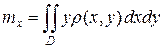, (19)

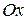называются статическими моментами плоской фигуры относительно осей и соответственно.

Дата добавления: 2015-10-30