Вероятностная постановка задачи обучения распознаванию двух классов объектов посредством выбора разделяющей гиперплоскости

Широкая популярность классического метода опорных векторов, изложенного в предыдущем разделе, объясняется его очень высокой устойчивостью в условиях малых обучающих совокупностей, многократно подтвержденной экспериментально. В то же время, этот метод обучения основан на чисто алгебраической идее искать решающее правило разделения объектов двух классов в виде некоторой гиперплоскости в пространстве их действительных признаков. Как следствие, решающее правило либо лишь указывает предполагаемый класс нового объекта, представленного своим вектором признаков , никак не комментируя достоверность такого решения.

Существует множество публикаций, в которых предлагаются разные варианты вероятностной интерпретации решающей функции , позволяющие трактовать ее значение для поступившего вектора признаков как апостериорную вероятность принадлежности соответствующего объекта к одному из двух классов, скажем, , после того, как получена и проанализирована обучающая совокупность . Однако все такие попытки неизбежно имеют искусственный характер, поскольку метод опорных векторов построен из чисто детерминистских соображений, и естественной основы для вероятностной оценки результатов его применения просто не существует.

В данном разделе мы поступим принципиально иным способом. Мы построим некоторую простейшую систему вероятностных предположений о паре плотностей распределения объектов двух классов, определяемой объективно существующей, но неизвестной гиперплоскостью в пространстве признаков, а также примем некоторое априорное предположение о случайном выборе самой неизвестной гиперплоскости. Далее мы покажем, что байесовское решение о скрытой разделяющей гиперплоскости, выведенное из случайной обучающей совокупности, приведет в точности к методу опорных векторов. Естественно, что при этом автоматически будет определена и апостериорная вероятность принадлежности всякого нового объекта к одному из двух классов.

Пусть в определена некоторая гиперплоскость с направляющим вектором и параметром сдвига , а также пара плотностей распределения вероятностей , , , , 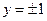сконцентрированных преимущественно по разные стороны от этой гиперплоскости. Плотности и выражают предположение, что случайные векторы признаков объектов двух классов 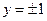распределены, главным образом, равномерно в «своих» полупространствах и , однако могут попадать и в «чужие» полупространства, причем степенью возможности «ошибочных» значений управляет параметр . Равномерное распределение в бесконечной области является некорректным вероятностным понятием, поэтому мы будем рассматривать несобственные плотности, не образующие единичного интеграла в области своего определения [[3]]:

Пара плотностей распределения, сконцентрированных в основном «равномерно» по разные стороны заданной гиперплоскости, выражает предположение, что единственное знание о двух классах объектов заключается в их расположении преимущественно по разные стороны заданной гиперплоскости в пространстве признаков, и нет никаких других предположений. Наглядное представление о такой паре плотностей распределения дает рис. 1,а.

Общий действительный параметр обеих плотностей , определяющий степень возможности попадания вектора признаков объекта определенного класса в «чужое» полупространство (рис. 1,б), будем считать структурным параметром сценария, имеющим известное заданное значение.

В свою очередь, направляющий вектор будем рассматривать как случайный, распределенный с некоторой известной плотностью . Никаких априорных предположений о значении случайного сдвига гиперплоскости мы принимать не будем, так что совместное распределение 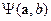будет рассматриваться как несобственное:

.

Далее, пусть обучающая совокупность есть результат многократных случайных независимых реализаций распределений и , всякий раз с известным индексом 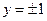принадлежности очередного объекта к одному из классов. Очевидно, что совместная условная плотность распределения векторов признаков объектов в составе обучающей совокупности относительно их известных классов выражается как произведение:

(а) (б)

Рис. 1. Яркостное представление несобственных плотностей распределения двух классов в двумерном пространстве признаков (а) и их значения вдоль направляющего вектора разделяющей гиперплоскости (б).

Апостериорное распределение параметров разделяющей гиперплоскости после наблюдения обучающей совокупности определяется формулой Байеса

,

а обучение естественно понимать как вычисление байесовской оценки параметров разделяющей гиперплоскости:

Подставляя в и, далее, в, мы получим критерий обучения:

Теорема 1. Критерий обучения эквивалентен следующему критерию:

Доказательство основано на замене переменных в, сумма которых для неправильно классифицированных объектов при текущих значениях и , подлежит минимизации вместе с , т.е. . Для остальных объектов, правильно классифицируемых при значениях и , сумма в критерий не входит, что позволяет записать его в виде

.

Но для неправильно классифицированных объектов , т.е. 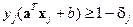. Если рассматривать эти неравенства как дополнительные ограничения, то минимизации подлежит критерий , совпадающий с.

Дата добавления: 2015-10-26