Априорные и апостериорные вероятности классов объектов

В вероятностной постановке задачи обучения, сформулированной в разделе 2.2.1, предполагалось, что классы объектов в составе обучающей совокупности заданы, поэтому нигде не возникал вопрос об априорных вероятностях принадлежности случайно появляющегося объекта одному либо другому классу.

Примем дополнительное предположение об этих априорных вероятностях:

, , .

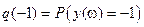Тогда, если считать параметры разделяющей гиперплоскости известными, то апостериорная вероятность принадлежности объекта с вектором признаков классу определяется формулой Байеса через плотности распределения двух классов :

.

В частности, если принять априорные вероятности обоих классов равными , то

,

и для принятых плотностей

Соответствующая зависимость от значения решающей функции показана на рис. 2.

Рис. 2. Апостериорные вероятности классов для вновь поступившего объекта
в вероятностной интерпретации метода опорных векторов.

2.2.3 Классический метод опорных векторов: Частный случай идентичных независимых нормальных априорных распределений элементов направляющего вектора с одной и той же известной дисперсией

Заметим, что критерий отличается от классического критерия метода опорных векторов лишь слагаемым вместо , зависящим от выбора априорной плотности распределения направляющего вектора разделяющей гиперплоскости. Примем дополнительное предположение, что это распределение является нормальным с нулевым математическим ожиданием и независимыми компонентами , характеризующимися одинаковыми дисперсиями :

.

В этом частном случае 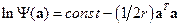. Умножив оба слагаемых в критерии на один и тот же коэффициент , мы получим классический критерий, в котором теперь коэффициент приобретает совершенно внятный смысл предполагаемой степени линейной разделенности двух классов объектов в пространстве их действительных признаков.

Очевидно, что масштаб измерения нормы направляющего вектора имеет условный характер, причем именно предполагаемая дисперсия его априори случайных компонент определяет этот масштаб. Степень «пересечения» областей концентрации распределений объектов одного и другого классов в пространстве признаков объектов, определяемую коэффициентом в модели, также следует понимать относительно этого масштаба. Уместно всегда предполагать априорную дисперсию равной единице , тогда смысл коэффициента 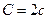в критерии метода опорных векторов полностью сводится к априорному предположению о степени пересечения классов в пространстве признаков объектов.

2.2.4 Обобщенный метод опорных векторов со взвешенными признаками: Идентичные независимые нормальные априорные распределения элементов направляющего вектора с известными разными дисперсиями

Предположим теперь, что компоненты направляющего вектора по-прежнему априори независимы и нормально распределены, но с разными априорными дисперсиями . Тогда, в отличие от, априорная плотность распределения будет иметь вид

.

В этом случае общий критерий обучения запишется в следующем виде:

Этот критерий отличается от классического критерия метода опорных векторов только наличием разных весов при компонентах искомого направляющего вектора в целевой функции вместо одинаковых идентичных весов .

Функция Лагранжа, соответствующая этой задаче квадратичного программирования, мало отличается от:

Эта функция Лагранжа приводит к несколько иной двойственной задаче обучения:

Отличие от заключается только в том, что в целевую функцию входят скалярные произведения векторов признаков объектов со взвешенными компонентами вместо исходных полных скалярных произведений .

Несколько иным получается и выражение оптимального направляющего вектора через векторы признаков объектов в обучающей совокупности

,

отличающемуся от 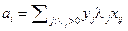тем, что каждая -я компонента направляющего вектора, по-прежнему являясь линейной комбинацией значений -го признака опорных объектов, вычисляется с весом, равным ее априорной дисперсии . Принцип обучения уместно называть взвешенным методом опорных векторов (weighted Support Vector Machine).

Последнее обстоятельство дает инструмент управления участием признаков в процессе обучения. Чем больше принятое значение априорной дисперсии некоторой компоненты направляющего вектора относительно априорных дисперсий других компонент, тем большее влияние -й признак оказывает на решение о классе объекта при использовании решающего правила , получаемого в результате обучения. Это особенно хорошо видно после подстановки в решающее правило:

Если , то -й признак вообще не участвует в принятии решения.

В следующей главе мы используем это обстоятельство для построения версии критерия обучения по методу опорных векторов, способной автоматически определять наиболее целесообразные значения весов признаков, т.е., в сущности, отбирать подмножество «полезных» признаков, подавляя «лишние».

3 Отбор подмножества информативных признаков в процессе обучения распознаванию двух классов объектов по методу опорных векторов:
Метод релевантных признаков

Дата добавления: 2015-10-26