Общий вид функции Лагранжа

Функция Лагранжа:

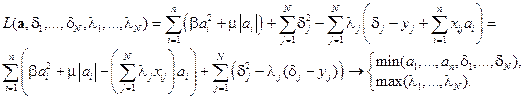
Выделим составляющие функции Лагранжа, зависящие от групп основных переменных и :

.

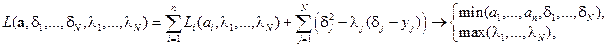
Ограничимся рассмотрением случая .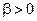

Проведем минимизацию функции Лагранжа по основным переменным и . Минимизация по дает:

Точка минимума недифференцируемой в нуле функции зависит от значения суммы по отношению к интервалу . Рассмотрим отдельно точки минимума функций в верхней и нижней строчках последнего выражения, т.е. на левой 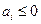и правой полуоси действительной переменной .

Если , то в верхней строчке коэффициент , и определяется условием

, т.е. ,

т.е. минимум достигается на левой полуоси 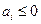. В нижней строчке в этом случае коэффициент даже отрицателен , и минимум

, т.е. ,

и минимум на правой полуоси не достигается, выходя из нее влево.

Если , то минимум функции на левой полуоси не достигается в ее пределах, уходя вправо 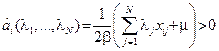. Аналогично, на правой полуоси минимум выходит из нее влево .

Наконец, если , то на левой полуоси точки минимума нет 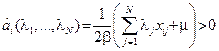, в то время как на правой полуоси точка минимума остается в ее пределах .

Итак:

В общем случае результат минимизации по :

Эквивалентная запись результата минимизации по при :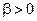

.

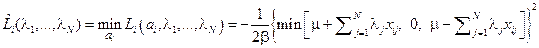Литература

[1]. Браверман Э.М. Опыты по обучению машины распознаванию зрительных образов. Автоматика и телемеханика, т. XXIII, № 3, 1962.

[2]. V. Vapnik. Statistical Learning Theory. John-Wiley & Sons, Inc., 1998, 736 p.

[3]. ДеГроот М. Оптимальные статистические решения. М.:, Мир, 1974.

[4]. L. Wang, J. Zhu, H. Zou. The doubly regularized support vector machine. Statistica Sinica, Vol. 16, 2006, pp. 589-615.

[5]. J. Zhu, S. Rosset, T. Hastie, R. Tibshirani. 1-norm Support Vector Machines. Advances in Neural Information Processing Systems, Cambridge, MA: MIT Press, 2004, vol. 16.

[6]. Сухарев А.Г., Тимохов А.В. Курс методов оптимизации. Учебное пособие. М.: Физматлит, 2005, 368 с.

[7]. G.C. Cawley, N.L.C. Talbot. Fast exact leave-one-out cross-validation of sparse least-squares support vector machines. Neural Networks, 2004, Vol. 17, pp. 1467-1475.

[8]. M.S. Bartlett. An inverse matrix adjustment arising in discriminant analysis. Annals of Mathema­tical Statistics, 1951, Vol. 22(1), pp. 1071-1111.

[9]. H. Zou and T. Hastie. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society, 67: 301-320, 2005.

[10]. R. Tibshirani. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, 58(1): 267-288, 1996.

Дата добавления: 2015-10-26