|
Читайте также: |
Линейные методы восстановления зависимостей по эмпирическим данным
В.В. Моттль
Вычислительный центр РАН
Московский физико-технический институт
О.С. Середин
Тульский государственный университет
Типовая задача восстановления закономерностей в множествах объектов реального мира
Некоторое множество реально существующих объектов 
.
Некоторое множество значений скрытой характеристики объектов 
.
Объективно существующая скрытая функция 
.
Желание наблюдателя:
Иметь инструмент оценивания скрытой характеристики для реальных объектов
; 
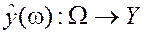– ошибка.
Обучение по прецедентам:
Подмножество наблюдаемых объектов, для которых измерено значение функции 
, 
.
Задача: Продолжить функцию на все множество 
, так чтобы можно было в дальнейшем оценивать значение рассматриваемой характеристики 
для новых объектов 
.
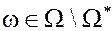Типовая задача восстановления закономерностей в множествах объектов реального мира
Некоторое множество реально существующих объектов .
Некоторое множество значений скрытой характеристики объектов .
Объективно существующая скрытая функция .
Желание наблюдателя:
Иметь инструмент оценивания скрытой характеристики для реальных объектов
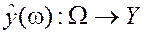; – ошибка.
Простейшие случаи:
Задача распознавания образов
– конечное неупорядоченное множество; в частности 
.
Задача восстановления числовой функции
– множество действительных чисел.
Концептуальная база восстановления зависимостей: гипотеза компактности
| Множество объектов реального мира Скрытая характеристика объекта (целевая характеристика) Искомое решающее правило | 
|
Основная идея:
Выбрать в множестве объектов некоторую метрику
, 
, если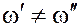 
, 
Принимать для близких объектов 
близкие решения
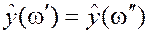в задаче распознавания образов
в задаче восстановления числовой зависимости
Выбор метрик удачен, если для них выполняется гипотеза компактности
(Эммануил Маркович Браверман, 1961):
Для пар объектов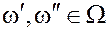 
, похожих в смысле выбранной метрики ,
значения целевой характеристики также в большинстве случаев близки 
.
Дата добавления: 2015-10-26; просмотров: 139 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Общий вид функции Лагранжа | | | Диполь в метрическом пространстве |