Соосность элементов метрического пространства

Метрическое пространство с метрикой :

, , если ;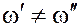

;

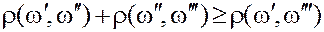– неравенство треугольника (равенство для некоторых троек)

Упорядоченная пара элементов 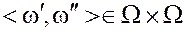, действительное число .

Элемент, соосный паре с коэффициентом

: ,

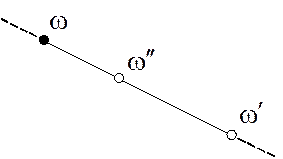
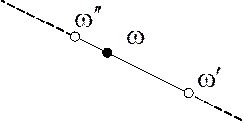
Соосность элементов метрического пространства

Метрическое пространство с метрикой :

, , если ;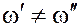

;

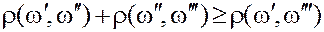– неравенство треугольника (равенство для некоторых троек)

Упорядоченная пара элементов 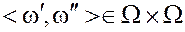, действительное число .

Элемент, соосный паре 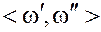с коэффициентом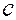

: ,

Метрическое пространство называется ординарным, если для каждой пары 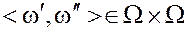и коэффициента существует не более одного элемента .

Неограниченно выпуклое метрическое пространство

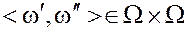Метрическое пространство называется неограниченно выпуклым, если для любой пары и любого коэффициента в нем существует элемент .

Неограниченно выпуклое метрическое пространство

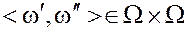Метрическое пространство называется неограниченно выпуклым, если для любой пары и любого коэффициента в нем существует элемент .

Идея введения линейных операций в ординарном неограниченно выпуклом метрическом пространстве

Центр метрического пространства .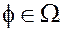

Умножение элемента на коэффициент	Сложение элементов

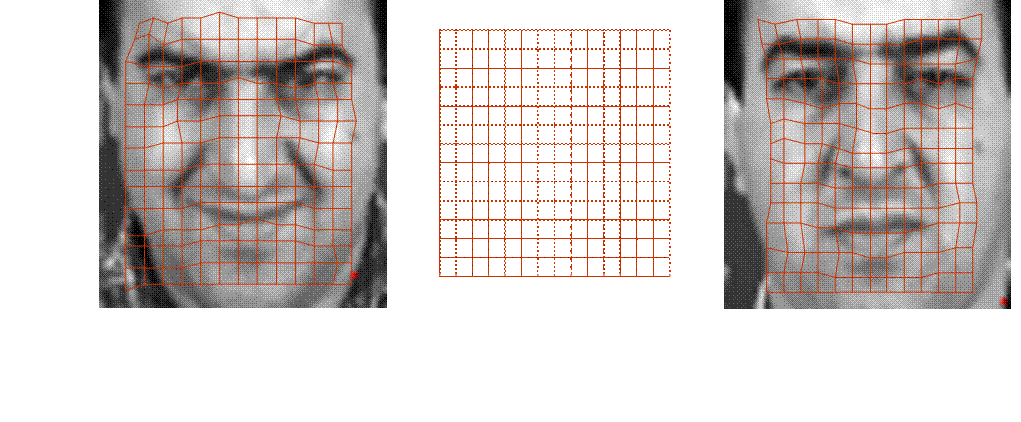
Пример «наивной» реализации линейных операций над изображениями

Пара изображений лица человека

изображение «среднее» изображение изображение

Метрика:

Пример «наивной» реализации линейных операций над изображениями

Пара изображений лица человека

изображение «среднее» изображение изображение

Метрика:

Пример «наивной» реализации линейных операций над изображениями

Пара изображений лица человека

изображение «среднее» изображение изображение

Метрика:

Пример «наивной» реализации линейных операций над изображениями

Пара изображений лица человека

изображение «среднее» изображение изображение

Оптимальная эластичная деформация растров пары изображений

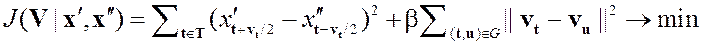
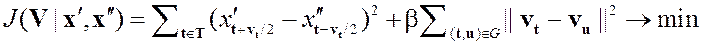
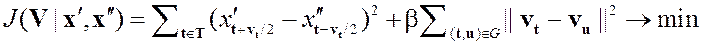
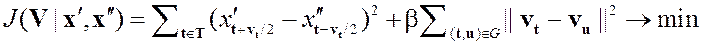
Метрика:

Дата добавления: 2015-10-26