
|
Читайте также: |
Аффинная комбинация конечной совокупности элементов евклидова метрического пространства 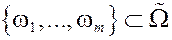 с коэффициентами
с коэффициентами  ,
,  :
:
 .
.
Евклидово расстояние между произвольным элементом  и заданной аффинной комбинацией
и заданной аффинной комбинацией  определяется выражением
определяется выражением
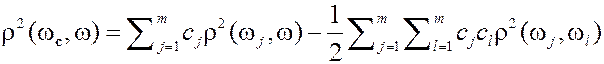
Наличие операции аффинной комбинации любого конечного числа элементов позволяет называть евклидово метрическое пространство  евклидовым аффинным пространством. От евклидова линейного пространства его отличает только отсутствие нулевого элемента. Если дополнительно назначить любой элемент в качестве нулевого
евклидовым аффинным пространством. От евклидова линейного пространства его отличает только отсутствие нулевого элемента. Если дополнительно назначить любой элемент в качестве нулевого  , то евклидова метрика
, то евклидова метрика 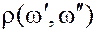 порождает в
порождает в  , во-первых, линейные операции сложения двух элементов и умножения элемента на действительный коэффициент, и, во-вторых, скалярное произведение (кернел):
, во-первых, линейные операции сложения двух элементов и умножения элемента на действительный коэффициент, и, во-вторых, скалярное произведение (кернел):  .
.
Евклидово аффинное пространство
Аффинная комбинация конечной совокупности элементов евклидова метрического пространства 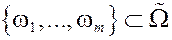 с коэффициентами
с коэффициентами  ,
,  :
:
 .
.
Евклидово расстояние между произвольным элементом  и заданной аффинной комбинацией
и заданной аффинной комбинацией  определяется выражением
определяется выражением
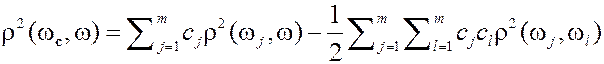
Наличие операции аффинной комбинации любого конечного числа элементов позволяет называть евклидово метрическое пространство  евклидовым аффинным пространством. От евклидова линейного пространства его отличает только отсутствие нулевого элемента. Если дополнительно назначить любой элемент в качестве нулевого
евклидовым аффинным пространством. От евклидова линейного пространства его отличает только отсутствие нулевого элемента. Если дополнительно назначить любой элемент в качестве нулевого  , то евклидова метрика
, то евклидова метрика 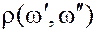 порождает в
порождает в  , во-первых, линейные операции сложения двух элементов и умножения элемента на действительный коэффициент, и, во-вторых, скалярное произведение (кернел):
, во-первых, линейные операции сложения двух элементов и умножения элемента на действительный коэффициент, и, во-вторых, скалярное произведение (кернел):  .
.
Евклидова метрика  порождает континуум разных линейных пространств и кернелов, но все они определяют одну и ту же исходную метрику
порождает континуум разных линейных пространств и кернелов, но все они определяют одну и ту же исходную метрику
 .
.
Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство
Евклидово метрическое (аффинное) пространство  с метрикой
с метрикой  .
.
Диполь 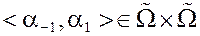 ,
, 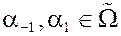 – узлы диполя.
– узлы диполя.
 – аффинная гиперплоскость.
– аффинная гиперплоскость.
Дата добавления: 2015-10-26; просмотров: 136 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Потенциальная функция (кернел) на множестве объектов, определяемая евклидовой метрикой | | | Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство |