Диполь в метрическом пространстве

Метрическое пространство объектов реального мира: , – метрика

Диполь в метрическом пространстве – упорядоченная пара: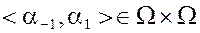

Простейшая реализация гипотезы компактности

Принадлежность произвольного объекта к одному из двух классов

Как выбрать диполь?

В множестве объектов слишком мало элементов. К тому же, наблюдатель располагает лишь конечной обучающей совокупностью объектов

Более «тонкая» реализация гипотезы компактности для непрерывного метрического пространства

– воображаемое непрерывное метрическое пространство, в котором множество реальных объектов является подмножеством, быть может, изолированных элементов.

, – метрическая гиперплоскость в

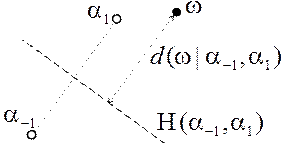
– проекция реального объекта на гиперплоскость в

Решающая функция (score function): расстояние точки от гиперплоскости в с учетом знака
	Классификация: Числовая зависимость:

Идеальные условия для реализации гипотезы компактности: Евклидова метрика в конечномерном линейном пространстве

Вектор действительных признаков погружает множество реальных объектов в

Естественная евклидова метрика в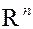

Диполь: , ; – направляющий вектор гиперплоскости

Смещенная гиперплоскость, определяемая диполем: ,

Решающая функция – decision (score) function: Расстояние от точки до гиперплоскости , при

Функция потерь: Степень несоответствия значения решающей функции значению целевой характеристики объекта

Индекс класса объекта Числовая характеристика
	Метод опорных векторов

Метод опорных векторов (Support Vector Machine – SVM): Принцип максимального зазора (margin) между классами

Обучающая совокупность , ,

	Требование максимизации зазора между линейно разделимыми классами
	Требование минимизации суммы штрафов

Компромисс:

Дата добавления: 2015-10-26