Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Пополнение метрического пространства с евклидовой метрикой

Читайте также:
  1. Адресные пространства
  2. ВВЕДЕНИЕ В КОРПУСКУЛЯРНУЮ ТЕОРИЮ ФАЗОВОГО ПРОСТРАНСТВА. ТЕРМОДИНАМИЧЕСКИЕ ВЕРОЯТНОСТИ И ПРОСТЕЙШЕЕ МОДЕЛИРОВАНИЕ МИКРОКАНОНИЧЕСКИХ АНСАМБЛЕЙ.
  3. Внутренний Дом и его пространства
  4. Времени и пространства
  5. Вселенная — это не “упакованный” контейнер; это система взаимоотношений между безграничными пространствами
  6. Вы за пределами пространства и времени
  7. Двойственная природа социального пространства

Множество объектов реального мира с евклидовой метрикой .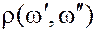

Если для какой-либо пары 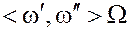и какого-либо коэффициента 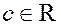в множестве не существует соосного элемента 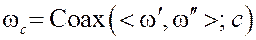, то расширим это множество, добавив в него такой элемент .

Пополнение метрического пространства с евклидовой метрикой

Множество объектов реального мира с евклидовой метрикой .

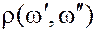Если для какой-либо пары 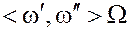и какого-либо коэффициента 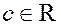в множестве не существует соосного элемента 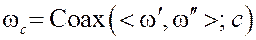, то расширим это множество, добавив в него такой элемент .

Так же поступим со всеми парами 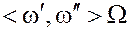, всеми числами 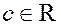, и со всеми парами, образуемыми полученными соосными элементами.

Пополнение метрического пространства с евклидовой метрикой

Множество объектов реального мира с евклидовой метрикой .

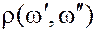Если для какой-либо пары 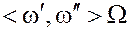и какого-либо коэффициента 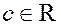в множестве не существует соосного элемента 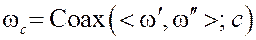, то расширим это множество, добавив в него такой элемент .

Так же поступим со всеми парами 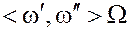, всеми числами 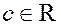, и со всеми парами, образуемыми полученными соосными элементами.

Результат: Гипотетическое метрическое пространство , неограниченное и выпуклое, содержащее исходное множество объектов реального мира.

Пополнение метрического пространства с евклидовой метрикой

Множество объектов реального мира с евклидовой метрикой .

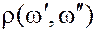Если для какой-либо пары 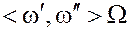и какого-либо коэффициента 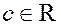в множестве не существует соосного элемента 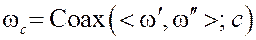, то расширим это множество, добавив в него такой элемент .

Так же поступим со всеми парами 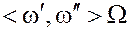, всеми числами 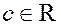, и со всеми парами, образуемыми полученными соосными элементами.

Результат: Гипотетическое метрическое пространство , неограниченное и выпуклое, содержащее исходное множество объектов реального мира.

Неограниченное выпуклое метрическое пространство с евклидовой метрикой будем называть евклидовым метрическим пространством.

Дата добавления: 2015-10-26; просмотров: 144 | Нарушение авторских прав

Читайте в этой же книге: Концептуальная база восстановления зависимостей: гипотеза компактности | Диполь в метрическом пространстве | Метод опорных векторов: Выпуклая форма критерия | Повтор: Диполь в метрическом пространстве | Соосность элементов метрического пространства | Евклидово аффинное пространство | Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство | Совокупность параметров, полностью определяющих выбор решающей функции |
<== предыдущая страница | следующая страница ==>
Пример «наивной» реализации линейных операций над изображениями| Потенциальная функция (кернел) на множестве объектов, определяемая евклидовой метрикой
mybiblioteka.su - 2015-2024 год. (0.009 сек.)