
Читайте также:
|

| Множество диполей единичной длины, определяющих одну и ту же дискриминантную гиперплоскость | ||
  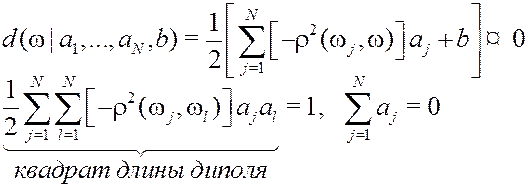
| 
| продольный сдвиг | |
| поворот | |||
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |

| Представление искомых узлов диполя:
 , ,  , ,
 . .
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |

| Представление искомых узлов диполя:
 , , 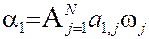 , ,
 . .
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |

| Представление искомых узлов диполя:
 , , 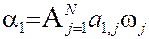 , ,
 . .
|
| В условиях принятых предположений достаточно искать дискриминантную функцию в виде | 
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |

| Представление искомых узлов диполя:
 , , 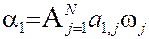 , ,
 . .
|
| В условиях принятых предположений достаточно искать дискриминантную функцию в виде | 
|
Эквивалентная формулировка задачи:

| Здесь не учтены ограничения на коэффициенты при объектах обучающей совокупности  , однако, как мы увидим ниже, решение задачи будет автоматически удовлетворять этим условиям. , однако, как мы увидим ниже, решение задачи будет автоматически удовлетворять этим условиям.
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |

| Представление искомых узлов диполя:
 , , 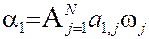 , ,
 . .
|
| В условиях принятых предположений достаточно искать дискриминантную функцию в виде | 
|
Эквивалентная формулировка задачи:

| Здесь не учтены ограничения на коэффициенты при объектах обучающей совокупности 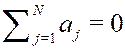 , однако, как мы увидим ниже, решение задачи будет автоматически удовлетворять этим условиям. , однако, как мы увидим ниже, решение задачи будет автоматически удовлетворять этим условиям.
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования |
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования |
Разделим обе части ограничений-неравенств во второй строке на  :
:

| Замена переменных: 
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования |
Разделим обе части ограничений-неравенств во второй строке на  :
:

| Замена переменных: 
|
Ограничения:

| Эквивалентная формулировка задачи  : :
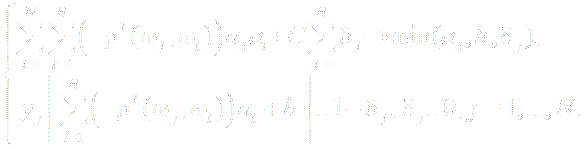
|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования |
Разделим обе части ограничений-неравенств во второй строке на  :
:

| Замена переменных: 
|
Ограничения:

| Эквивалентная формулировка задачи 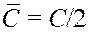 : :

|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования |
Двойственная задача:
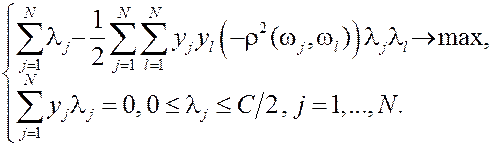
| Для сравнения: двойственная задача Kernel-based SVM

|
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования

|
Двойственная задача:
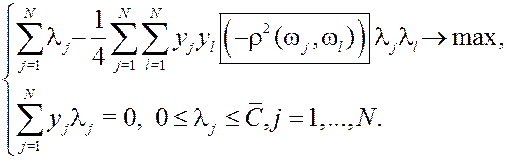
| Для сравнения: двойственная задача Kernel-based SVM

|
Решение: 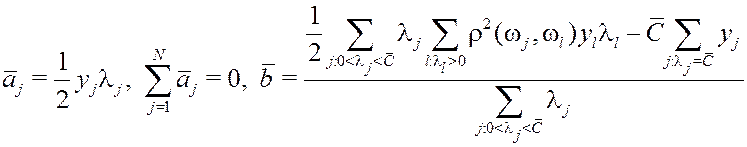
Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)
Обучающая совокупность: 
| |
Эквивалентная формулировка задачи:

| Это задача квадратичного программирования

|
Двойственная задача:
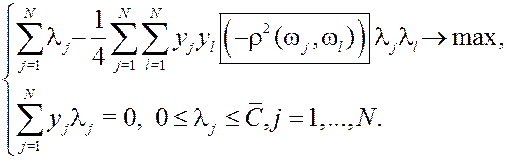
| Для сравнения: двойственная задача Kernel-based SVM

|
Правило классификации нового объекта:
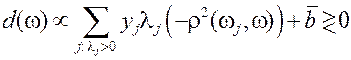
| Правило классификации нового объекта:
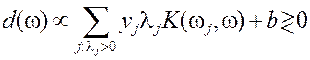
|
Задача обучения для произвольной функции попарного сравнения объектов: Relational Dependence Estimation
Доступна лишь функция попарного сравнения объектов 
Обучающая совокупность: 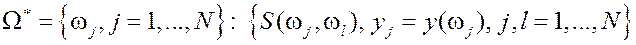
Вектор вторичных признаков объекта  относительно обучающей совокупности:
относительно обучающей совокупности: 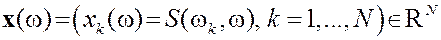 .
.
Классический критерий обучения SVM:

| Обучение проводится по  объектам обучающей совокупности, представленным объектам обучающей совокупности, представленным  вторичными признаками относительно обучающих (базисных) объектов. вторичными признаками относительно обучающих (базисных) объектов.
|
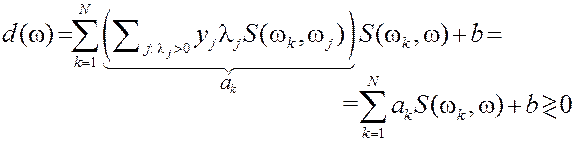 В дискриминантной функции участвуют все объекты обучающей совокупности (R. Duin: Relational Discriminant Analysis)
В дискриминантной функции участвуют все объекты обучающей совокупности (R. Duin: Relational Discriminant Analysis)
| Результат обучения:
Дискриминантная функция, применимая к произвольному объекту 
|
Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты  , игнорируя остальные
, игнорируя остальные  .
.
Искомое решающее правило: 
Идея Tipping&Bishop: Априорное вероятностное представление об искомом векторе коэффициентов 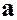
|  чем меньше
чем меньше  , тем ближе априори , тем ближе априори 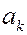 к нулю к нулю
|
Дополнительное предположение Tipping&Bishop: Меры точности  также априори независимы, случайны и распределены по гамма закону также априори независимы, случайны и распределены по гамма закону
| 
|
Если 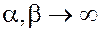 и и  , то гамма-распределение , то гамма-распределение  к равномерному на к равномерному на 
| 
|
Полное априорное распределение вектора коэффициентов 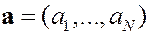 :
:

Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты  , игнорируя остальные
, игнорируя остальные  .
.
Искомое решающее правило: 
Идея Tipping&Bishop: Априорное вероятностное представление об искомом векторе коэффициентов 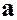
|  чем меньше
чем меньше  , тем ближе априори , тем ближе априори 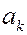 к нулю к нулю
|
Дополнительное предположение Tipping&Bishop: Меры точности  также априори независимы, случайны и распределены по гамма закону также априори независимы, случайны и распределены по гамма закону
| 
|
Полное априорное распределение вектора коэффициентов 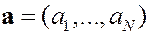 :
:
 ,
,  близко к равномерному распределению
близко к равномерному распределению
| Регуляризованный критерий обучения | 
|
Далее Tipping&Bishop применяют ЕМ-алгоритм. При этом приходится прибегать к эвристикам из-за наличия ограничений типа неравенств. Задача невыпукла.
Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты  , игнорируя остальные
, игнорируя остальные  .
.
Искомое решающее правило: 
Идея Tipping&Bishop: Априорное вероятностное представление об искомом векторе коэффициентов 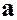
|  чем меньше
чем меньше  , тем ближе априори , тем ближе априори 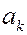 к нулю к нулю
|
Дополнительное предположение Tipping&Bishop: Меры точности  также априори независимы, случайны и распределены по гамма закону также априори независимы, случайны и распределены по гамма закону
| 
|
Полное априорное распределение вектора коэффициентов 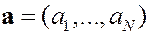 :
:
 ,
,  близко к равномерному распределению
близко к равномерному распределению
| Регуляризованный критерий обучения | 
|
Такой метод обучения крайне селективен по отношению к базисным объектам –
в качестве релевантных остаются лишь очень малое число объектов.
Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
 Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты
Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты  , игнорируя остальные
, игнорируя остальные  .
.
Искомое решающее правило: 
Идея Tipping&Bishop: Априорное вероятностное представление об искомом векторе коэффициентов 
|  чем меньше
чем меньше  , тем ближе априори , тем ближе априори 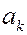 к нулю к нулю
|
Дополнительное предположение Tipping&Bishop: Меры точности 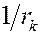 также априори независимы, случайны и распределены по гамма закону также априори независимы, случайны и распределены по гамма закону
| 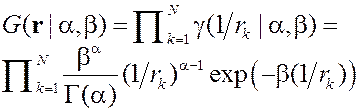
|
Полное априорное распределение вектора коэффициентов 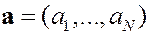 :
:
 ,
, 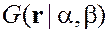 близко к равномерному распределению
близко к равномерному распределению
| Регуляризованный критерий обучения | 
|
Такой метод обучения крайне селективен по отношению к базисным объектам –
в качестве релевантных остаются лишь очень малое число объектов.
Обучение для заданной функции попарного сравнения с отбором базисных объектов: Relevance Object Machine
 Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты
Michael Tipping, Christopher Bishop: Оставить лишь наиболее информативные (релевантные) базисные объекты  , игнорируя остальные
, игнорируя остальные  .
.
Искомое решающее правило: 
Идея Tipping&Bishop: Априорное вероятностное представление об искомом векторе коэффициентов 
|  чем меньше
чем меньше  , тем ближе априори , тем ближе априори 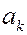 к нулю к нулю
|
Дополнительное предположение Tipping&Bishop: Меры точности 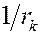 также априори независимы, случайны и распределены по гамма закону также априори независимы, случайны и распределены по гамма закону
| 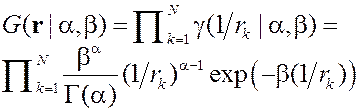
|
Полное априорное распределение вектора коэффициентов 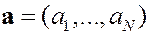 :
:
 ,
, 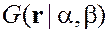 близко к равномерному распределению
близко к равномерному распределению
| Регуляризованный критерий обучения | 
|
Relevance Vector Machine – RVM, поскольку в качестве функции парного сравнения объектов  Tipping&Bishop использовали кернел, погружающий множество объектов в линейное пространство, где они рассматриваются как векторы.
Tipping&Bishop использовали кернел, погружающий множество объектов в линейное пространство, где они рассматриваются как векторы.
Дата добавления: 2015-10-26; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство | | | ЛИНЕЙНЫЕ ПРОСТРАНСТВА |