Линейные пространства

Учебно-методическое пособие

Томск

РАССМОТРЕНО и УТВЕРЖДЕНО методической комиссией факультета прикладной математики и кибернетики.

ПРОТОКОЛ № 20 от 14 июня 2004 г.

Председатель комиссии

профессор С.Э.Воробейчиков

В учебно-методическом пособии приведены краткие теоретические сведения и даны практические рекомендации к решению задач по курсу «Линейная алгебра и аналитическая геометрия».

Пособие разработано для студентов факультета прикладной математики и кибернетики дневной формы обучения.

Составители: К.И.Лившиц

Л.Ю.Сухотина

1. Линейные пространства. Определение

Определение. Множество X называется линейным пространством над полем K, если:

1. Существует закон, который позволяет каждым двум элементам 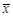, поставить в соответствие элемент , называемый суммой и обозначаемый

2. Существует закон, который позволяет каждому элементу 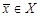и каждому числу поставить в соответствие элемент , называемый «произведением элемента 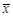на число » и обозначаемый

3. Законы, введенные в X, удовлетворяют следующим аксиомам:

1. ,

2. ,

3.

4. :

5.

6.

7.

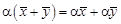
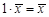
8. , где 1 — единица поля K.

Элементы пространства X обычно называют векторами, элемент — нулевым вектором, элемент — противоположным (обратным) к вектору .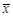

Из определения непосредственно вытекают следующие элементарные свойства линейного пространства:

1. В любом линейном пространстве существует единственный .

2. В любом линейном пространстве для каждого элемента существует единственный противоположный элемент.

3. Для всякого вектора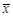

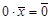
4. Для всякого вектора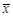

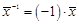
Примеры:

1. Рассмотрим множество квадратных матриц n -го порядка с вещественными элементами. Поле K — поле вещественных чисел. Законы сложения элементов и умножения на число определены в матричном анализе. Из свойств сложения матриц и умножения матрицы на число следует выполнение аксиом 1—8. В частности, является нулевая матрица n -го порядка. Следовательно, данное множество есть линейное пространство.

2. Линейным пространством является также множество V ₃ геометрических векторов, операции над которыми были определены в векторном анализе. Поле K – поле вещественных чисел. Сами проверьте, что аксиомы 1—8 выполняются.

3. Рассмотрим множество P_n, элементами которого являются упорядоченные наборы из n вещественных чисел.

Поле K — поле вещественных чисел. Сложение и умножение на число определяется следующим образом. Если , то , если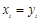

Сами проверьте выполнение аксиом 1—8. Нулевой вектор в данном случае это упорядоченный набор n нулей . Данное пространство называется арифметическим пространством.

Задачи

Проверить образуют ли следующие множества линейные пространства. Операции сложение элементов и умножение на число определены общепринятым образом. Поле K — поле вещественных чисел.

1. Множество n- мерных симметричных матриц с вещественными элементами.

2. Множество n- мерных кососимметричных матриц с вещественными элементами.

3. Все векторы плоскости, концы которых лежат на данной прямой, а начало совпадает с началом системы координат.

4. Все векторы плоскости, начала и концы которых лежат на данной прямой.

5. Все многочлены степени от одного неизвестного с вещественными коэффициентами.

6. Все многочлены степени n от одного неизвестного с вещественными коэффициентами.

2. Линейная зависимость.
Базис и координаты вектора.

Рассмотрим линейное пространство X над полем K. Пусть , . Линейной комбинацией векторов пространства X называется сумма вида

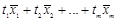
Числа называются коэффициентами линейной комбинации.

Определение. Элементы пространства X называются линейно зависимыми, если существуют числа не все равные нулю одновременно такие, что линейная комбинация

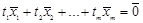(2.1)

Если же равенство (2.1) выполнено только тогда, когда все числа , то векторы называются линейно независимыми.

Необходимым и достаточным условием линейной зависимости векторов является равенство одного из них линейной комбинации других.

Примеры

1. Рассмотрим пространство геометрических векторов V ₃. В нем два вектора линейно зависимы, когда они коллинеарны; три вектора линейно зависимы, когда они компланарны. Всякие четыре вектора этого пространства всегда линейно зависимы.

2. Рассмотрим арифметическое пространство R_n. Попытаемся построить линейно независимую систему векторов этого пространства. Рассмотрим k векторов

,

Если линейно зависимы, то одновременно такие, что

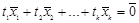
где – ноль пространства R_n. По определению R_n отсюда следует, что

,

Получаем в результате относительно t_i систему n линейных однородных уравнений с k неизвестными и матрицей размера . Такая система имеет только нулевое решение, если

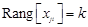
и имеет ненулевое решение, если

Отсюда следует, что в пространстве R_n не может быть больше, чем n линейно независимых векторов. Линейно независимыми являются всякие векторы, компоненты которых образуют матрицу полного ранга. Например, n векторов

(2.2)

Определение. Совокупность линейно независимых векторов 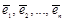пространства X называется базисом этого пространства, если найдутся такие числа , что справедливо равенство

(2.3)

Соотношение (2.3) называется разложением вектора 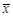по базису.

В силу линейной независимости векторов базиса разложение (2.3) определяется единственным образом.

Определение. Коэффициенты 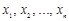разложения вектора 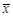по базису называются координа­тами вектора 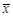относительно базиса.

Пример. Совокупность векторов (2.2) образует очевидно базис пространства R_n, так как для всякого вектора имеет место разложение

При решении задач полезно помнить, что векторы линейно зави­симы тогда и только тогда, когда линейно зависимы вектор-столбцы из их координат относительно произвольного базиса.

Определение. Если в линейном пространстве X существует n линейно независимых векторов, а всякие век­тор этого пространства линейно зависимы, то число, n называется размерностью линейного пространства

Само линейное пространство X называется при этом n -мерным. Линейное пространство, в котором можно указать сколь угодно большое число линейно независимых векторов называется бесконечно мерным.

Примеры

1. Пространство V ₃. В этом пространстве вся­кие три некомпланарных вектора линейно независимы, а всякие че­тыре вектора линейно зависимы. Следовательно, .

2. Пространство R_n. В этом пространстве всякие вектор линейно зависимы и существуют системы из n линейно независимых векторов, например, система векторов (2). Следовательно,

Если в линейном пространстве X существует базис из n векторов, то , обратно, если , то вся­кая система из n линейно независимых векторов образует базис пространства X.

Всякие два базиса и пространства X связаны между собой симметричными формулами

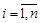(2.4)

(2.5)

где невырожденные матрицы 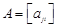и являются взаимно обратными, i -й столбец матрицы A образуют координаты вектора в базисе из векторов . Формулы (2.4) и (2.5) называются формулами перехода, матрицы A и — матрицами перехода.

Если и – координаты вектора 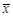в базисах и , соответственно, то

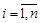(2.6)

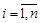(2.7)

Пример: Доказать, что каждая из данных двух систем векторов является базисом R ₃ и найти связь координат одного и того же вектора 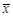в этих двух базисах:

Для доказательства того, что данные системы векторов являются базисными, вычислим, как и в предыдущем примере, ранги матриц

и

Нетрудно убедиться, что , и, следовательно, в R ₃ данные системы векторов образуют базисы. Для определения связи координат необходимо получить формулы перехода (2.4) и (2.5). Имеем

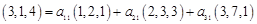
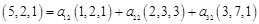
Откуда получаем систему девяти скалярных уравнений

Решая системы уравнений, получаем матрицу перехода

и связь между «старыми» и «новыми» координатами:

Задачи

1. Доказать, что если система векторов содер­жит нулевой вектор, то совокупность векторов линейно зависима.

2. Доказать, что если часть из векторов линейно зависима, то и вся эта совокупность векторов линейно зависима.

Векторы и 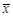заданы своими координатами в некотором базисе. Показать, что векторы сами образуют базис и найти координаты вектора 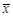в этом базисе:

3.

, , ,

4.

, , ,

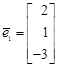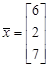
5.

, , , ,

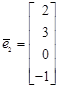6. Доказать, что каждая из двух систем векторов является базисом, и найти связь координат одного и того же вектора в этих двух базисах.

, , ,

, , ,

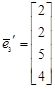7. Доказать линейную независимость системы функций , где – попарно различные действительные числа.

8. Определить размерность линейного пространства квадратных матриц n -го порядка.

9. Как изменится матрица перехода от одного базиса к другому, если:

а) поменять местами два вектора первого базиса;

б) поменять местами два вектора второго базиса;

в) записать векторы обоих базисов в обратном порядке?

Дата добавления: 2015-10-26