
Читайте также:
|
| Невыпуклый критерий | Замена переменных |

| 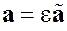 , ,  , тогда , тогда 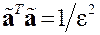
|
| Результат замены: | 
|
Выпуклый критерий обучения:
Задача квадратичного программирования
 переменных, переменных,  ограничений ограничений
| 
|
Метод опорных векторов: Выпуклая форма критерия
Выпуклый критерий обучения:
Задача квадратичного программирования
 переменных, переменных,  ограничений ограничений
| 
| ||
Двойственная форма задачи:
Задача квадратичного программирования
 соответствуют обучающим объектам соответствуют обучающим объектам 
| 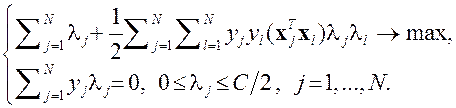
|

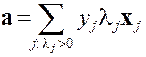 ,
,  ,
, 
Правило классификации нового объекта 
Эквивалентная запись 
Метод опорных векторов: Выпуклая форма критерия
Выпуклый критерий обучения:
Задача квадратичного программирования
 переменных, переменных,  ограничений ограничений
| 
| ||
Двойственная форма задачи:
Задача квадратичного программирования
 соответствуют обучающим объектам соответствуют обучающим объектам 
| 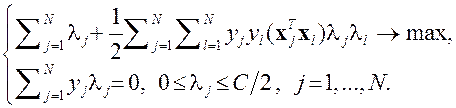
|

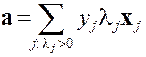 ,
,  ,
, 
Правило классификации нового объекта 
Эквивалентная запись 
Метод опорных векторов: Выпуклая форма критерия
Выпуклый критерий обучения:
Задача квадратичного программирования
 переменных, переменных,  ограничений ограничений
| 
| ||
Двойственная форма задачи:
Задача квадратичного программирования
 соответствуют обучающим объектам соответствуют обучающим объектам 
| 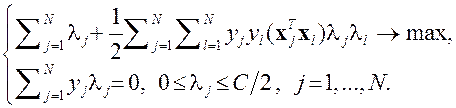
|

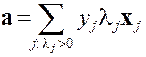 ,
,  ,
, 
Правило классификации нового объекта 
Эквивалентная запись 
Метод опорных векторов: Выпуклая форма критерия
Выпуклый критерий обучения:
Задача квадратичного программирования
 переменных, переменных,  ограничений ограничений
| 
| ||
Двойственная форма задачи:
Задача квадратичного программирования
 соответствуют обучающим объектам соответствуют обучающим объектам 
| 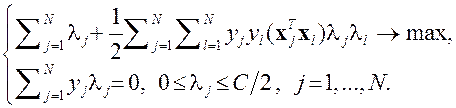
|

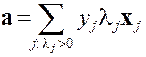 ,
,  ,
, 
Правило классификации нового объекта 
Эквивалентная запись 
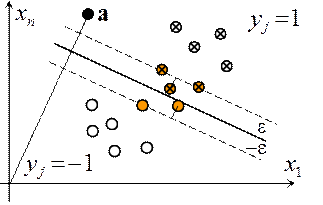
| Метод опорных векторов Support Vector Machine (SVM) |
Повтор: Диполь в метрическом пространстве
Метрическое пространство объектов реального мира:  ,
,  – метрика
– метрика
Диполь в метрическом пространстве – упорядоченная пара: 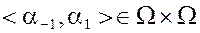
Дата добавления: 2015-10-26; просмотров: 128 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Диполь в метрическом пространстве | | | Повтор: Диполь в метрическом пространстве |