Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство

Евклидово метрическое (аффинное) пространство с метрикой .

Диполь 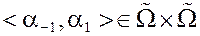, 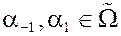– узлы диполя.

– аффинная гиперплоскость.

– произвольный элемент евклидова метрического пространства,
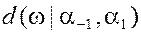– его расстояние до аффинной гиперплоскости с учетом знака.

Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство

Евклидово метрическое (аффинное) пространство с метрикой .

Диполь 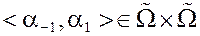, 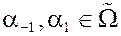– узлы диполя.

– аффинная гиперплоскость.

– произвольный элемент евклидова метрического пространства,
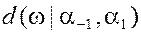– его расстояние до аффинной гиперплоскости с учетом знака.

Теорема. .

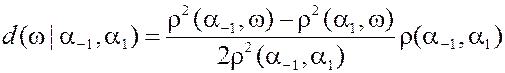Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство

Евклидово метрическое (аффинное) пространство с метрикой .

Диполь , 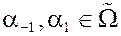– узлы диполя.

– аффинная гиперплоскость.

– произвольный элемент евклидова метрического пространства,
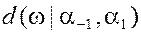– его расстояние до аффинной гиперплоскости с учетом знака.

Теорема. .

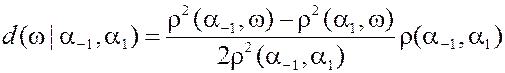Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)

Обучающая совокупность:
	Представление искомых узлов диполя: ,

Диполь и аффинная гиперплоскость в евклидовом метрическом (аффинном) пространство

Евклидово метрическое (аффинное) пространство с метрикой .

Диполь , 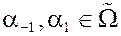– узлы диполя.

– аффинная гиперплоскость.

– произвольный элемент евклидова метрического пространства,
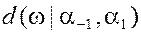– его расстояние до аффинной гиперплоскости с учетом знака.

Теорема. .

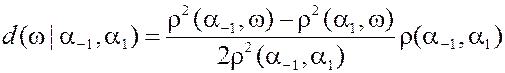Задача обучения распознаванию объектов двух классов:
Принцип максимизации зазора (аналог задачи SVM)

Обучающая совокупность:
	Представление искомых узлов диполя: ,

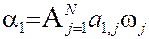
Совокупность параметров, полностью определяющих выбор решающей функции

Дата добавления: 2015-10-26