Двойственная задача обучения

Функция Лагранжа:

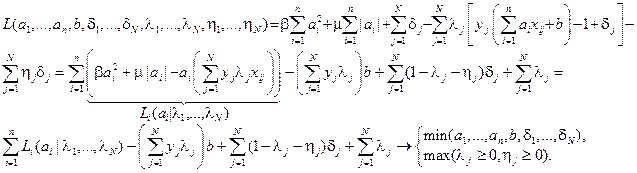
Здесь 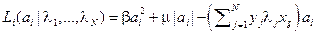. Минимизация функции Лагранжа по 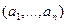сводится к минимизации по 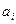каждой из функций

.

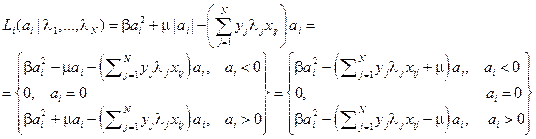Ограничимся рассмотрением случая .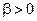

Точка минимума 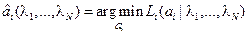недифференцируемой в нуле функции 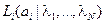зависит от значения 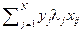по отношению к интервалу .

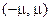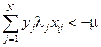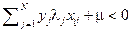Если , то и 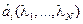определяется условием

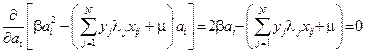т.е. .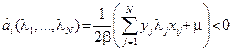

Если 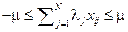, то .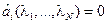

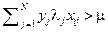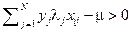Если , то , и 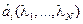определяется условием

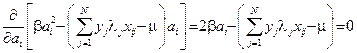, т.е. .

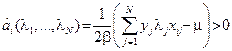Сведем вместе все три варианта:

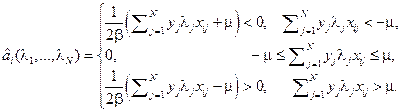
Результат минимизации по 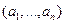согласно и:

.

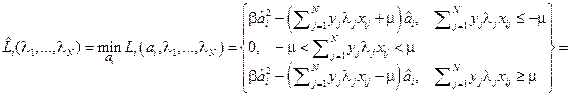
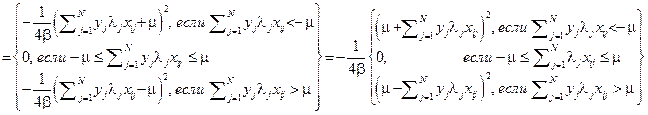Заметим, что в первом случае 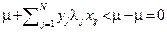и 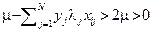, а в последнем случае 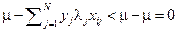и 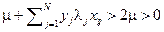, поэтому

.

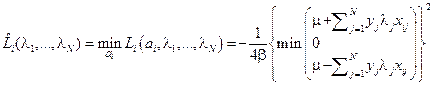Отсюда следует эквивалентная запись результата минимизации по :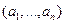

.

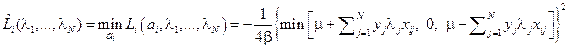Минимизация функции Лагранжа по остальным целевым переменным 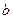и 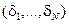не отличается от случая классического критерия SVM, и, и приводит к равенствам

,

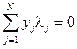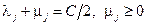, т.е. , .

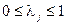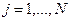Подстановка, и в выражение для функцию Лагранжа приводит к устранению целевых переменных и дает двойственную задачу обучения:

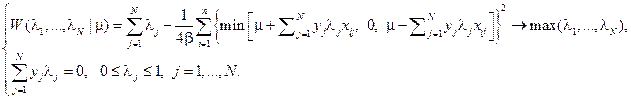
После того, как двойственная задача обучения решена, и найдены значения множителей Лагранжа 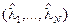, значения компонент направляющего вектора 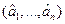оптимальной разделяющей гиперплоскости определяются равенствами. Если обозначить через 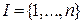все множество признаков объектов 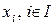, т.е. множество компонент направляющего вектора 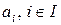, то решение двойственная задачи 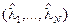согласно разбивает это множество на три подмножества , , , :

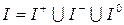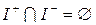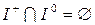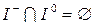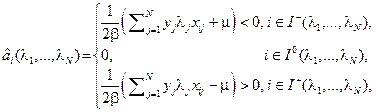
где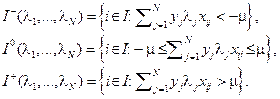

Селективность обучения заключается в том, что часть признаков 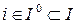объявляются неактивными в решающем правиле распознавания, применимом к произвольным объектам 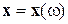, в том числе к тем, которые не участвовали в обучении:

.

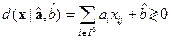Смещение гиперплоскости 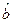определяется теми же соображениями -, что и для классического критерия обучения SVM:

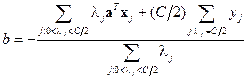
Целевая функция двойственной задачи является вогнутой кусочно-квадратичной функцией, подлежащей максимизации в выпуклой области. Численное решение двойственной задачи может быть получено подходящим стандартным итерационным методом выпуклого (вогнутого) программирования, например, методом внутренней точки [[6]]. Однако специфика эадачи позволяет построить более простой итерационный алгоритм ее численного решения, опирающийся на любой метод решения более простой задачи квадратичного программирования, предполагающей, что целевая функция является квадратичной вместо более общего случая вогнутой функции.

Дата добавления: 2015-10-26