Линейная модель числовой зависимости. Центрированная и нормированная обучающая совокупность

Продолжим рассмотрение идеальной ситуации, когда вектор действительных признаков 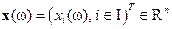, , 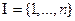погружает множество реальных объектов 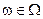в конечномерное линейное пространство 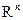(раздел 1.5). Однако будем говорить о задаче восстановления числовой зависимости, когда множество значений скрытой характеристики объектов есть числовая ось 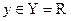, а модель зависимости ищется в линейном виде

.

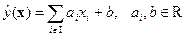Если задана обучающая совокупность 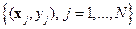, то задача оценивания линейной модели зависимости в условиях излишне большого множества числовых признаков объектов 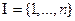, , 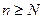может быть сформулирована как задача построения модели гребневой регрессии, заключающаяся в совместной взвешенной минимизации остаточной суммы квадратов ошибок 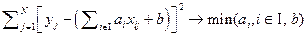и так называемого гребневого регуляризующего штрафа 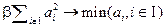, где 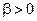– коэффициент баланса между этими взаимно противоречивыми требованиями. Однако очевидно, что гребневой штраф имеет смысл, только если обучающая совокупность центрирована и нормирована:

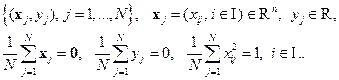
В противном случае регуляризующий штраф должен быть идтвтдуальным 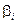для каждого признака 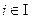, чтобы компенсировать различие масштабов их измерения.

Если 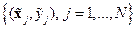– исходная обучающая совокупность, то она может быть нормализована следующим образом:

.

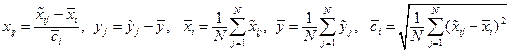Обратно, если по нормализованной обучающей совокупности найдена регрессионная модель 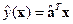, то ее следует пересчитать в исходные шкалы, в которых естественным образом измерены признаки нового объекта 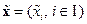. Согласно 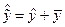, поэтому

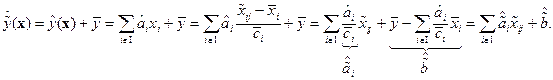
В предположении, что обучающая совокупность центрирована и нормирована, задача гребневого обучения (Ridge Regression) примет следующий вид:

.

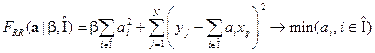Критерий гребневой регрессии содержит два структурных параметра – гребневой штраф 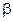и подмножество признаков 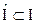. Выбор первого из них не составляет серьезной проблемы, достаточно принять достаточно малое значение 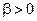с единственной целью гарантировать строгую выпуклость критерия обучения в случае возможной линейной зависимости подвекторов признаков в 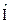. Однако что качается выбора подмножества 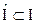, то это очень трудная задача.

Оценить «качество» конкретного подмножества признаков 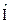можно по методу скользящего контроля, который для квадратичного критерия допускает простую численную реализацию [[7]], основанную на известной матричной формуле (Sherman-Woodbury-Morrison formula) [[8]]. Однако перебрать все 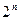подмножеств 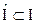все равно невозможно.

Дата добавления: 2015-10-26