Алгоритм обучения с заданной селективностью отбора признаков

Критерий обучения по методу опорных векторов с релевантными компонентами несложно алгоритмически реализовать, разделив все множество варьируемых переменных на два подмножества и с применением метода итерационного попеременного спуска (метода Гаусса-Зайделя). Итерационный процесс естественно начать, например, с исходных единичных значений .

Пусть на очередной итерации 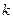получены значения . Тогда оптимизация по сводится к минимизации обобщенного критерия опорных векторов со взвешенными признаками:

Для найденного приближения к искомому направляющему вектору оптимизация по сводится к решению независимых задач:

, .

Приравнивание производной по дает условие

Здесь существенным является только условие равенства нулю выражения в скобках, поскольку побочное условие вытекает из того, что положительная производная целевой функции в пределе уменьшается до нуля при достаточно больших значениях , и целевая функция в целом имеет только одну точку минимума. Как следствие, очередные значения дисперсий компонент направляющего вектора определяются отношениями

.

В частности, из последней формулы хорошо видно, что при нулевой селективности оценки всех дисперсий тождественно равны единице , и критерий вырождается в обычный критерий опорных векторов, сохраняющий все признаки.

При правило вычисления значений дисперсий на очередной итерации принимает вид

.

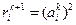В этом случае алгоритм подавляет почти все признаки, оставляя один, редко два из них.

Что же касается выбора наиболее подходящего значения параметра селективности , то это выбор нельзя сделать ни из каких байесовских соображений, поскольку всегда максимальное значение совместного апостериорного распределения подлежащих оцениванию параметров модели данных будет наибольшим при самой «широкой» модели, т.е. при нулевой селективности. Значение параметра , как и любого структурного параметра модели, следует, используя тот либо иной критерий кросс-валидации на основе деления обучающей совокупности на основную и контрольную подвыборки.

4 Отбор подмножества информативных признаков в процессе обучения распознаванию двух классов объектов по методу опорных векторов:
Метод опорных признаков

Дата добавления: 2015-10-26