Определение двойного интеграла

Задача об объёме цилиндрического тела

Введём в пространстве прямоугольную систему координат Oxyz. Рассмотрим в плоскости Oxy конечную замкнутую область D, границей которой является замкнутая кривая Г. Построим на Г как на направляющей линии цилиндрическую поверхность с образующими, параллельными оси Oz.

Пусть в области D определена непрерывная положительная функция точки , графиком которой является поверхность , располагающаяся над плоскостью Oxy. Тело, ограниченное сверху поверхностью , снизу – областью D в плоскости Oxy, с боков – цилиндрической поверхностью, будем называть цилиндрическим телом. Вычислим его объём.

Разобьём область D на n непересекающихся элементарных областей с площадями соответственно. Тогда всё цилиндрическое тело окажется разбитым на элементарные цилиндрические столбики с основаниями , и его объём будет равен сумме их объёмов: .

Вычислим приближённо объём 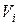i -го столбика, для чего выберем внутри области 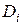произвольную точку и «срежем» столбик параллельно плоскости Oxy на высоте . Тогда , и объём приближённо будет равен

. (1)

Ясно, что чем меньше размеры элементарных областей , тем точнее формула (1) представляет объём цилиндрического тела. Назовём диаметром области 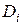наибольшее из расстояний между точками этой области: . Если теперь увеличивать до бесконечности число разбиений n, так чтобы величина стремилась к нулю, то приближённое равенство (1) в пределе станет точным:

. (2)

Формула (2) представляет искомый объём цилиндрического тела.

Определение двойного интеграла

Назовём сумму вида (1) интегральной суммой для функции , соответствующей данному разбиению области D на элементарные области 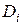и данному выбору точек в каждой из этих областей. Меняя способ разбиения и способ выбора точек, можно составить бесконечное множество таких интегральных сумм.

Определение. Число 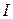называется пределом интегральных сумм при 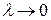, если для любого числа существует такое число , что для всех интегральных сумм , у которых 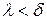, выполняется неравенство при любом выборе точек в элементарных областях .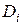

Предел 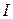, если он существует, называется двойным интегралом от функции по области и обозначается символом . Функция называется интегрируемой в области , а область – областью интегрирования.

Таким образом, по определению двойной интеграл, как и определённый интеграл, есть предел интегральных сумм:

. (3)

Вопрос. Для каких функций и областей двойной интеграл заведомо существует?

Ответ. Теорема (достаточное условие существования двойного интеграла). Если функция непрерывна в замкнутой ограниченной области , то она интегрируема в .

Возвращаясь к задаче об объёме цилиндрического тела, заключаем, что если фигурирующая в ней функция интегрируема в области , то объём (2) равен двойному интегралу от функции по области :

. (4)

В этом состоит геометрический смысл двойного интеграла.

Дата добавления: 2015-10-30