
|
Читайте также: |
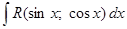 .
.
Запись 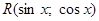 означает, что над синусом и косинусом производятся только рациональные операции: сложение и вычитание, умножение на постоянные величины, возведение в целые степени как положительные, так и отрицательные, деление. Другими словами, под символом
означает, что над синусом и косинусом производятся только рациональные операции: сложение и вычитание, умножение на постоянные величины, возведение в целые степени как положительные, так и отрицательные, деление. Другими словами, под символом 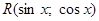 следует понимать рациональную функцию синуса и косинуса.
следует понимать рациональную функцию синуса и косинуса.
Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью, так называемой универсальной тригонометрической подстановки
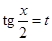 .
.
В результате этой подстановки имеем:
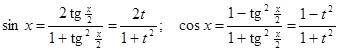 ;
;
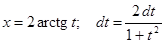 .
.
Задача V.V.1. Найти интегралы: 1) 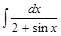 ; 2)
; 2) 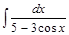 ; 3)
; 3) 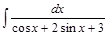 ; 4)
; 4) 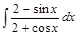 .
.
1) ▲ 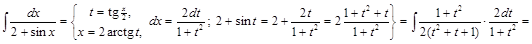
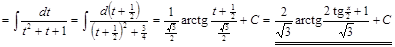 . ▼
. ▼
2) ▲ 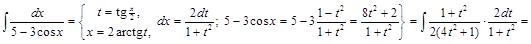
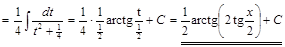 . ▼
. ▼
3) ▲ 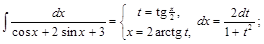
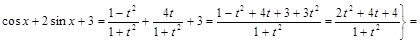
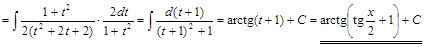 . ▼
. ▼
4) ▲ 
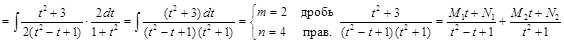
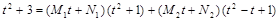
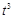
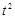
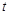
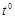
| 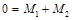
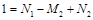
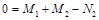
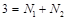
| 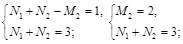 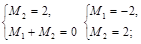
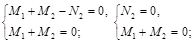 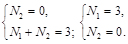
|
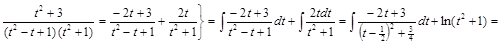
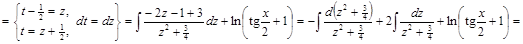
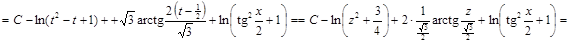
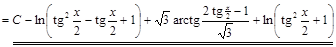 . ▼
. ▼
Универсальная подстановка 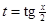 приводит во многих случаях к сложным вычислениям, так как при ее применении
приводит во многих случаях к сложным вычислениям, так как при ее применении 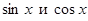 выражаются через переменную
выражаются через переменную 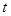 в виде рациональных дробей, содержащих
в виде рациональных дробей, содержащих 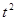 .
.
В ряде случаев рационализация подынтегрального выражения может быть достигнута с помощью других, более простых подстановок. Приведем важнейшие из этих случаев.
Если подынтегральная функция имеет вид
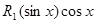 ,
,
где 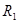 – рациональная функция одного аргумента, то применяется подстановка
– рациональная функция одного аргумента, то применяется подстановка
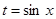 .
.
Замечание. Если функция 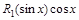 меняет знак при замене
меняет знак при замене 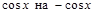 ,
,
т. е. является нечетной функцией 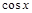 , то применяется подстановка
, то применяется подстановка 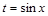 .
.
Если подынтегральная функция имеет вид
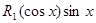 ,
,
где 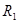 – рациональная функция одного аргумента, то применяется подстановка
– рациональная функция одного аргумента, то применяется подстановка
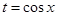 .
.
Замечание. Если функция 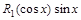 меняет знак при замене
меняет знак при замене 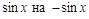 ,
,
т. е. является нечетной функцией 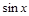 , то применяется подстановка
, то применяется подстановка 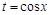 .
.
3. Если функция 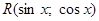 не изменяется при замене
не изменяется при замене 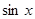 на
на 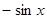 и
и
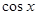 на
на 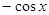 , т. е.
, т. е. 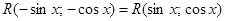 ,
,
то для нахождения интеграла целесообразно использовать подстановку 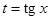 .
.
Задача V.V.2. Найти интегралы: 1) 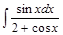 ; 2)
; 2) 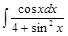 ; 3)
; 3) 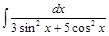 .
.
1) ▲ 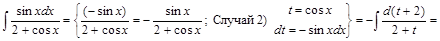
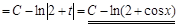 . ▼
. ▼
2) ▲ 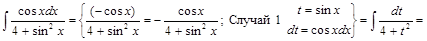
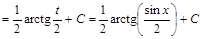 . ▼
. ▼
3) ▲ 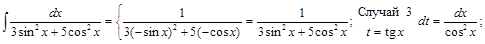
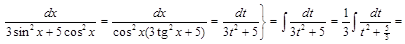
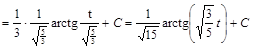 . ▼
. ▼
Решение задач 22-24, 26 типового варианта
Найти неопределенные интегралы.
1) ▲ 
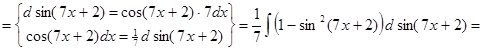
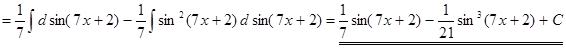 . ▼
. ▼
2) ▲ 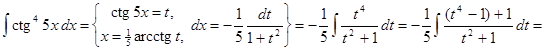
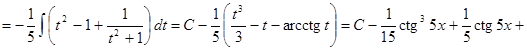
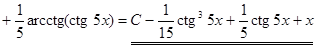 . ▼
. ▼
3) ▲ 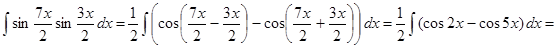
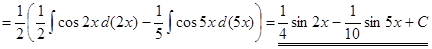 . ▼
. ▼
4) ▲ 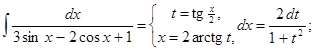
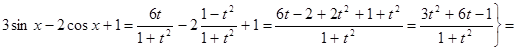
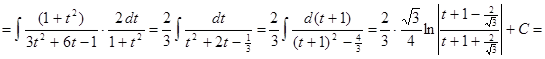
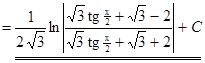 . ▼
. ▼
VI. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
В отличие от функций рациональных иррациональные выражения далеко не всегда интегрируются в элементарных функциях. Рассмотрим некоторые частные типы иррациональных функций, интегрирующихся в конечном виде.
Дата добавления: 2015-10-30; просмотров: 116 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| II. Интегралы вида | | | VI. ИНТЕГРИРОВАНИЕ РАЗНЫХ ФУНКЦИЙ |