Основные приемы и методы интегрирования

УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ

ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Р Г Г М У

Санкт-Петербург

Одобрено Научно-методическим советом РГГМУ

УДК 51

Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Неопределенный интеграл. – СПб.: Изд. РГГМУ. 2007. – 57 с.

Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок.

Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.

© Веретенников В. Н.

© Российский государственный гидрометеорологический университет (РГГМУ), 2006.

ПРЕДИСЛОВИЕ

"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями.

Целью математического образования является:

1. Воспитание достаточно высокой математической культуры.

2. Привитие навыков современных видов математического мышления.

3. Привитие навыков использования математических методов и основ математического моделирования в практической деятельности.

Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.

В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Неопределенный интеграл"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.

ОСНОВНЫЕ ПРИЕМЫ И МЕТОДЫ ИНТЕГРИРОВАНИЯ

Основная задача дифференцирования:

Дана функция 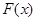. Найти .

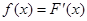Основная задача интегрирования:

Дана производная функции 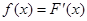. Найти .

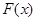Интегрирование – операция, обратная дифференцированию.

Определение. Функция 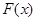называется первообразной функцией или первообразной по отношению к функции 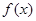на некотором промежутке 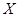, если функция 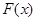дифференцируема в каждой точке этого промежутка и ее производная 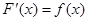или, что то же самое, .

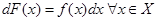В связи с понятием первообразной сразу же возникают два вопроса:

1. для каких функций можно гарантировать существование первообразной?

2. сколько первообразных может иметь одна и та же функция?

Ответ на первый вопрос дается теоремой

Теорема 1 (о существовании первообразной). Если функция 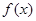непрерывна на некотором промежутке 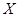, то на этом промежутке у нее существует первообразная.

Ответ на второй вопрос содержится в следующей теореме.

Теорема 2. Если 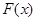– какая-нибудь первообразная функции 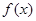на некотором промежутке, то формула

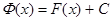, (1)

где 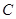– любая постоянная, дает общий вид первообразных для функции .

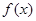Иными словами, здесь утверждается, что всякая функция вида (1) – первообразная для функции 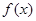, и, обратно, всякая первообразная для функции 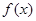имеет вид (1) при надлежащем подборе постоянной .

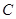Определение. Если функция 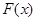– первообразная для функции 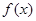на промежутке 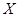, то множество функций 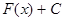, где 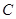– произвольная постоянная, называется неопределенным интегралом от функции 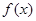на этом промежутке.

Обозначение: .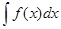

Таким образом, имеем

.

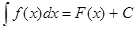Дата добавления: 2015-10-30