Vi. Интегрирование разных функций

Ранее рассматривались в основном интегралы определенного типа и соответствующие способы их нахождения. Найти – значит определить тип интеграла и избрать наиболее эффективный способ решения. Сначала остановимся на некоторых общих положениях, а затем приведем соответствующие примеры.

Встречаются случаи, когда один и тот же интеграл можно найти различными способами. Ясно, что в первую очередь следует применить тот способ, который быстрее приведет к окончательному результату (в частности, способ подведения под знак дифференциала).

При нахождении заданного интеграла иногда необходимо сначала сделать замену переменной, а затем уже применить соответствующий способ интегрирования.

Многие интегралы с разными по виду подынтегральными функциями находят с помощью интегрирования по частям.

Решение ряда прикладных задач связано с нахождением неопределенных интегралов, при этом не всегда встречаются интегралы рассмотренных видов или которые приведены в справочниках. Еще требуется выполнить некоторые тождественные преобразования, чтобы перейти от рассматриваемого интеграла к интегралу известного типа (особенно это относится к интегралам, содержащим тригонометрические и гиперболические функции).

Интегрирование выражений, содержащих гиперболические функции, аналогично интегрированию выражений, содержащих тригонометрические функции, и часто связано с применением формул:

.

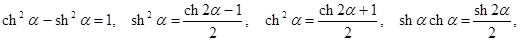
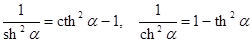В процессе обучения и в практической деятельности возникает необходимость обращаться к справочникам, содержащим таблицы интегралов.

Задача 1. Найти интегралы: 1) 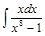; 2) .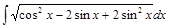

1) ▲

. ▼

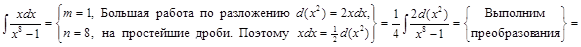
2) ▲

. ▼

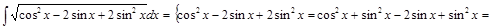
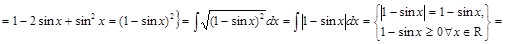
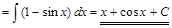Интегралы вида

.

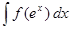Применим подстановку . .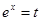

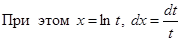Данный интеграл сводится к интегралу вида .

Задача 2. Найти интегралы: 1) 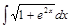; 2) .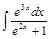

1) ▲

. ▼

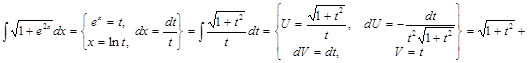
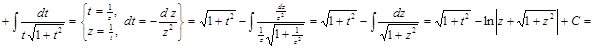
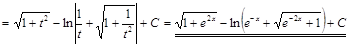2) ▲

. ▼

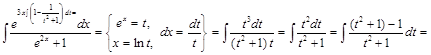
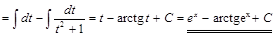Еще раз напоминаем, что один и тот же интеграл можно найти по-разному

Задача 3. Найти интегралы: 1) 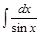; 2) .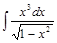

1) ▲ Способ 1.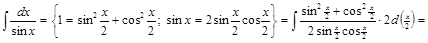

.

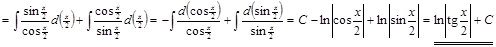Способ 2. .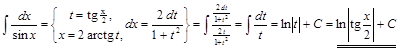

Способ3. . ▼

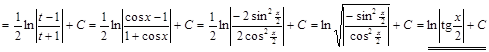2) ▲ Способ 1.

.

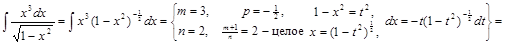
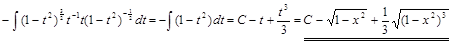Способ 2.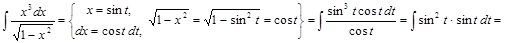

.

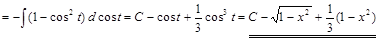Способ 3.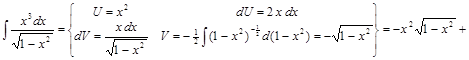

. ▼

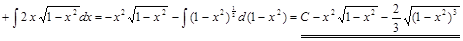Дата добавления: 2015-10-30