Некоторые корни знаменателя кратные

Задача IV.2. Разложить на простейшие дроби рациональную дробь .

▲ Данная дробь правильная .

1) Знаменатель уже разложен на множители и имеет два различных вещественных корня: кратности 3 и .

2) Разложение данной дроби на простейшие имеет вид

.

3) Приводя правую часть этого равенства к общему знаменателю, и приравнивая числители в его левой и правой частях, получим тождество

.

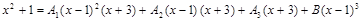В правой части произведем умножение двучленов и получим

.

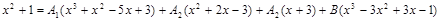Это равенство можно переписать иначе, расположив многочлен в правой части по убывающим степеням :

.

4) Для определения неизвестных коэффициентов применим способ частных значений в сочетании со способом неопределенных коэффициентов (будем в дальнейшем называть его комбинированным). Напоминаем, что написанное равенство является тождеством: оно остается верным при любом значении . Принимая и 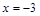, мы сможем определить два коэффициента. Далее сравним коэффициенты в левой и правой части тождества. В результате имеем:

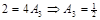
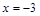
Искомым разложением будет

. ▼

Некоторые корни знаменателя – комплексные числа

Задача IV.3. Разложить на простейшие дроби рациональную дробь .

▲ Данная дробь правильная .

Разложим знаменатель на множители: .

Квадратичный множитель вещественных корней не имеет, а потому имеет место разложение

.

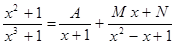Умножая обе части равенства , получаем

Для определения неизвестных коэффициентов применим комбинированный метод

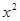
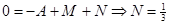
Искомое разложение имеет вид

.

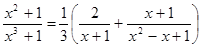Корни знаменателя – кратные комплексные числа

Задача IV.4. Разложить на простейшие дроби рациональную дробь .

▲ Данная дробь правильная .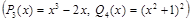

1) Знаменатель уже разложен на множители и не имеет вещественных корней.

2) Поэтому разложение на простейшие дроби должно иметь вид

.

3) Умножая обе части равенства , получаем

или .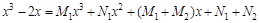

4) Для определения неизвестных коэффициентов применим метод неопределенных коэффициентов. Приравнивая коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, будем иметь

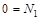
5) Следовательно, . ▼

Замечание - свободный член.

Дата добавления: 2015-10-30