Несобственные интегралы с бесконечными пределами интегрирования.

Несобственные интегралы.

Понятие определенного интеграла было дано в предположении, что отрезок интегрирования конечен, а подынтегральная функция ограничена на этом отрезке. Если хотя бы одно из этих условий нарушено, то соответствующие интегралы называются несобственными. Рассмотрим два вида несобственных интегралов.

Несобственные интегралы с бесконечными пределами интегрирования.

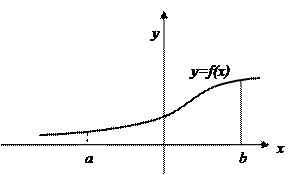
Пусть промежутком интегрирования является луч , а функция y=f(x) интегрируема на каждом конечном отрезке [a,b]. Геометрически задача состоит в нахождении площади под кривой. Возьмем точку в, найдем площадь кр.тр.через опр. инт. и устремим в к .

Несобственным интегралом

называют предел функции верхнего предела интегрирования при его стремлении к бесконечности:

= .

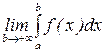Если указанный предел существует и конечен, то говорят, что несобственный интеграл существует или сходится, если конечный предел не существует – то говорят, что несобственный интеграл не существует или расходится.

Пусть теперь промежутком интегрирования является луч .

Тогда аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом:

= .

Аналогично определяется несобственный интеграл с двумя бесконечными пределами. В этом случае числовую ось разбивают произвольной точкой с на два луча и полагают

+ .

Если оба несобственных интеграла в правой части сходятся, то сходится и несобственный интеграл в левой части, причем его значение не зависит от выбора промежуточной точки с (доказать самостоятельно).

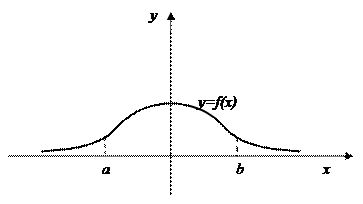
В геометрическом смысле несобственный интеграл от неотрицательной функции равен площади неограниченной криволинейной трапеции.

Пример 1. .

Данный несобственный интеграл расходится.

Пример 2. .

Данный несобственный интеграл сходится к значению 1.

Заметим, что указанный способ нахождения несобственных интегралов можно свести к применению аналога формулы Ньютона-Лейбница:

= .

Пример 3. .

Дата добавления: 2015-10-30