
|
Читайте также: |
(6) Если 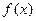 непрерывна при
непрерывна при 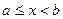 ,
, 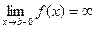 , то несобственным интегралом от разрывной функции называют
, то несобственным интегралом от разрывной функции называют

(7) Если 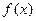 непрерывна при
непрерывна при  ,
,  , то
, то 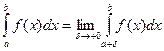
(8) Если 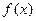 непрерывна при
непрерывна при  , кроме точки
, кроме точки 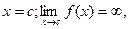 то
то 
(9) 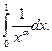 При
При  интеграл существует (сходится), при
интеграл существует (сходится), при 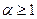 интеграл расходится
интеграл расходится
(10) Признак сходимости и расходимости несобственных интегралов 2-го рода (признак сравнения): если 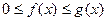 при
при 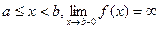 , то из сходимости
, то из сходимости 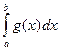 следует сходимость
следует сходимость  , из расходимости
, из расходимости  следует расходимость
следует расходимость 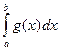
Гамма-функция
(11) 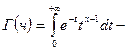 сходится при x >0
сходится при x >0
(12) 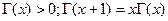 при
при 
(13) 

Значения некоторых несобственных интегралов
(14) 
(15) 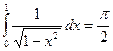
(16) 
(17) 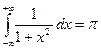
(18) 
(19) 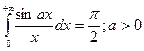
(20) 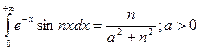
Литература
Учебники
1. Письменный Д.Т. Конспект лекций по высшей математике; Полный курс. — М.: АЙРИС ПРЕСС, 2004. — 608 с.: ил. ISBN 5-8112-0508-2
2. Зайцев, И.А. Высшая математика. — М.: Изд. Дрофа, 2004, — 400 с. ISBN 5-7107-6957-6?5-7107-9071-0
3. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2008. — 479 c. ISBN 978-5-06-006050-8
4. Берман А.Ф., Араманович И.Г. Краткий курс математического анализа для ВТУЗов. – М.: Изд. Лань, 2008. — 736 с. ISBN 978-5-8114-1499-5
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1,2. — М.: НАУКА Главная редакция физико-математической литературы, 1978.
Пособия по решению задач
6. Данко П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. I. Учебное пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Е. Кожевников. – 6-е изд. — М.: Издательский дом «ОНИКС 21 век»: Мир и образование, 2003. – 304 с., ил. ISBN 5-329-00528-0
7. Данко П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. II. Учебное пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Е. Кожевников. – 6-е изд. — М.: Издательский дом «ОНИКС 21 век»: Мир и образование, 2003. – 416 с., ил. ISBN 5-329-00528-0
Задачники
8. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. — 3-е изд., испр. и доп. — М.: Айрис-пресс, 2004. — 576 с.: ил. — (Высшее образование). ISBN 5-8112-0552-X
9. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты: Учебное пособие. 6-е изд., стер. / Л.А. Кузнецов. – СПб.: Издательство «Лань», 2005. – 240 с. — (Учебники для вузов. Специальная литература). ISBN 5-8114-0574-X
10. Демидович Б.П. Задачи и упражнения по математическому анализу. — М.: «Наука» Главная редакция физико-математической литературы, 1986.
11. Минорский В.П. Сборник задач по высшей математике. — М.: «Наука», Главная ред. физмат литературы. 1987
Справочники
12. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов.– 13-е изд., исправленное./ И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, Гл. ред. физ. – мат. лит., 1986.– 544 с.
13. Выгодский, М.Я. Справочник по высшей математике. — 14-е изд. / М.Я. Выгодский. — М.: «ДЖАНГАР», «БОЛЬШАЯ МЕДВЕДИЦА», 2001. 864 с. ISBN 57102-0197-9
* При затруднении в ответах на эти вопросы рекомендуем обратиться к теоретической части курса.
Дата добавления: 2015-10-30; просмотров: 184 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление площадей, длин дуг и объемов с помощью определенного интеграла | | | SECTION D - TO THE HEAD TEACHER/PRINCIPAL OF THE APPLICANT'S SCHOOL |